Spread-location and spread-level plots

The eda_sl function generates William Cleveland's spread-location plot for univariate and bivariate data. The function will also generate Tukeys' spread-level plot.

Usage

eda_sl(
  dat,
  x = NULL,
  fac = NULL,
  type = "location",
  p = 1,
  tukey = FALSE,
  base = exp(1),
  sprd = "frth",
  jitter = 0.01,
  robust = TRUE,
  loess.d = list(family = "symmetric", degree = 1, span = 1),
  label = TRUE,
  label.col = "lightsalmon",
  xlab = NULL,
  ylab = NULL,
  labelxbuff = 0.05,
  labelybuff = 0.05,
  show.par = FALSE,
  plot = TRUE,
  ...
)

Arguments

dat

Dataframe of univariate data or a linear model.

x

Continuous variable column (ignored if dat is a linear model).

fac

Categorical variable column (ignored if dat is a linear model).

type

s-l plot type. "location" = spread-location, "level" = spread-level (only for univariate data). "dependence" = spread-dependence (only for bivariate model input).

p

Power transformation to apply to variable. Ignored if input is a linear model.

tukey

Logical; Determines if a Tukey transformation should be adopted (FALSE adopts a Box-Cox transformation).

base

Base used with the log() function if px or py is 0.

sprd

Choice of spreads used in the spread-versus-level plot (i.e. when type = "level"). Either interquartile, sprd = "IQR" or fourth-spread, sprd = "frth" (default).

jitter

Jittering parameter for the spread-location plot. A fraction of the range of location values.

robust

Logical; Indicates if robust regression should be used on the spread-level plot.

loess.d

Arguments passed to the internal loess function. Applies only to the bivariate model s-l plots and the spread-level plot.

label

Logical; Determines if group labels are to be added to the spread-location plot.

label.col

Color assigned to group labels (only applicable if type = location).

xlab

X label for output plot.

ylab

Y label for output plot.

labelxbuff

Buffer to add to the edges of the plot to make room for the labels in a spread-location plot. Value is a fraction of the plot width.

labelybuff

Buffer to add to the top of the plot to make room for the labels in a spread-location plot. Value is a fraction of the plot width.

show.par

Boolean determining if the power transformation applied to the data should be displayed.

plot

Logical; Determines if plot should be generated.

...

Arguments passed on to .eda_plot_xy

y: A numeric vector or column name in dat for the y-axis.
px: Power transformation used in the input data to display if show.par = TRUE.
py: Power transformation used in the input data to display if show.par = TRUE.
raw_tick: Logical. If TRUE, original (untransformed) equally spaced tick values are displayed on the re-expressed axes.
xlim: X-axis range.
ylim: Y-axis range.
reg: Logical; whether to fit and display a regression line.
poly: Integer; regression model polynomial degree (defaults to 1 for linear model).
rlm.d: List; parameters for MASS::rlm, (e.g., list(psi = "psi.bisquare")).
w: Optional numeric vector of weights for regression.
lm.col: Regression line color.
lm.lw: Numeric; Regression line width.
lm.lty: Numeric; Regression line type.
sd: Logical; whether to show ±1 SD lines.
mean.l: Logical; whether to show x and y mean reference lines.
asp: Logical; whether to preserve the aspect ratio (ignored if square = FALSE).
square: Logical; whether to create a square plotting window.
grey: Numeric between 0-1; controls grayscale background elements (0 = black, 1 = white).
pch: Integer; point symbol.
p.col: Point border color.
p.fill: Point fill color.
size: Point size.
alpha: Point transparency level (0 = 100\% transparent, 1 = 100\% opaque).
q: Logical; whether to draw inner quantile boxes (quantile shading).
q.type: Integer; type of quantile calculation (see quantile).
inner: Numeric; defines the inner fraction of values to highlight with quantile shading.
qcol: Fill color of quantile shading.
loe: Logical; whether to plot loess smooth line.
loe.lw: Numeric; Loess smooth line width.
loe.col: Loess smooth color.
loe.lty: Numeric; Loess smooth line type.
stats: Logical; if TRUE, displays model statistics (R², β, p-value).
stat.size: Text size for stats plot display.
hline: Numeric; location(s) of additional horizontal reference lines. Can be passed via the c() function.
vline: Numeric; location(s) of additional vertical reference lines. Can be passed via the c() function.

Value

Returns a dataframe of level and spread values.

Details

The function generates a few variations of the spread-location/spread-level plots depending on the data input type and parameter passed to the type argument. The residual spreads are mapped to the y-axis and the levels are mapped to the x-axis. Their values are computed as follows:

type = "location" (univariate data):

William Cleveland's spread-location plot applied to univariate data.
\(\ spread = \sqrt{|residuals|}\)
\(\ location = medians\)
type = "level" (univariate data):

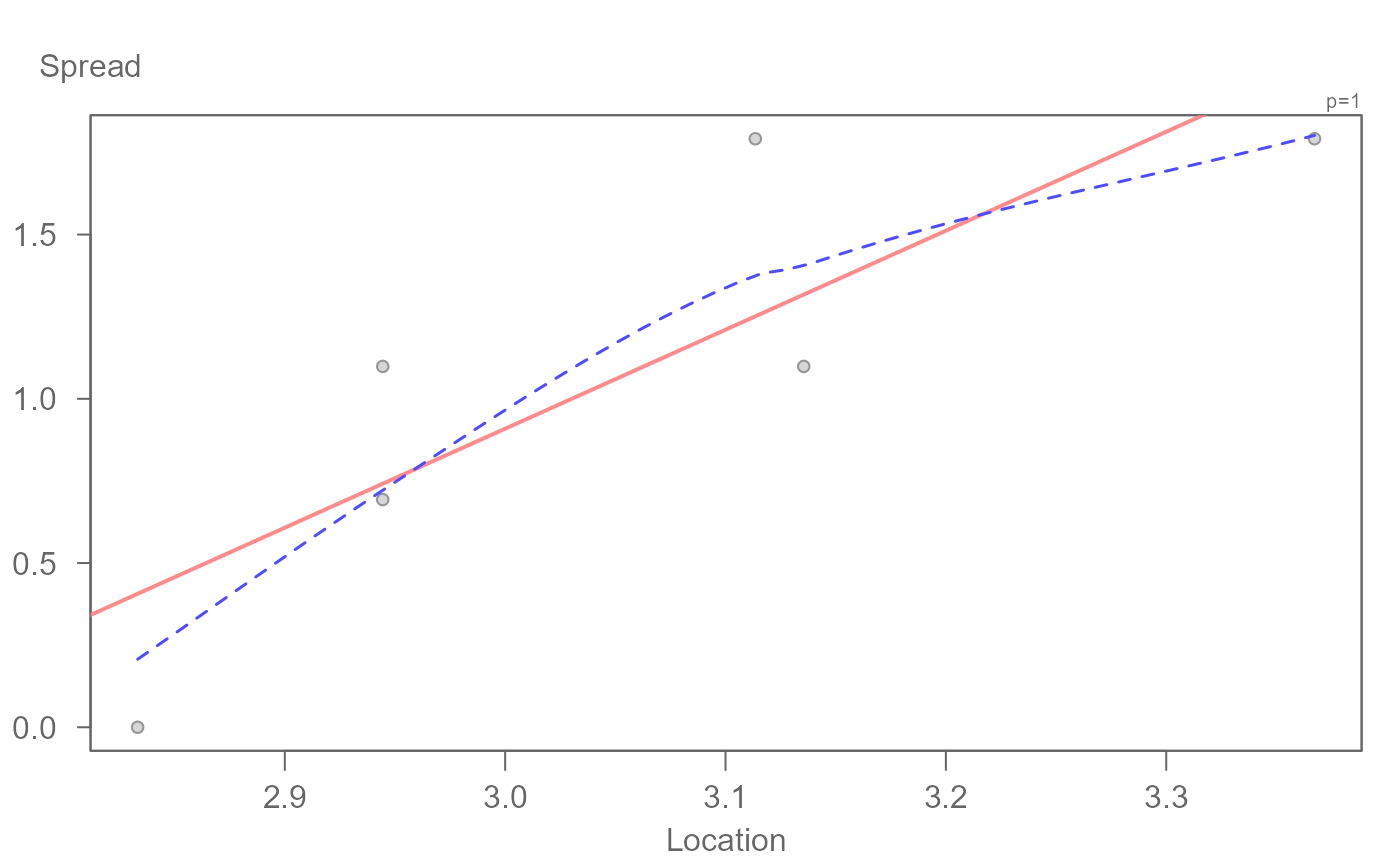
Tukey's spread-level plot (aka spread-versus-level plot, Hoaglin et al., p 260). If the pattern is close to linear, the plot can help find a power transformation that will help stabilize the spread in the data by subtracting one from the fitted slope. This option outputs the slope of the fitted line in the console. A loess is added to assess linearity. By default, the fourth spread is used to define the spread. Alternatively, the IQR can be used by setting spread = "IQR". The output will be nearly identical except for small datasets where the two methods may diverge slightly in output.
\(\ spread = log(fourth\ spread(residuals))\)
\(\ location = log(medians)\)
type = "location" if input is a model of class lm, eda_lm or eda_rline:

William Cleveland's spread-location plot (aka scale-location plot) applied to residuals of a linear model.
\(\ spread = \sqrt{|residuals|}\)
\(\ location = fitted\ values\)
type = "dependence" if input is a model of class lm, eda_lm or eda_rline:

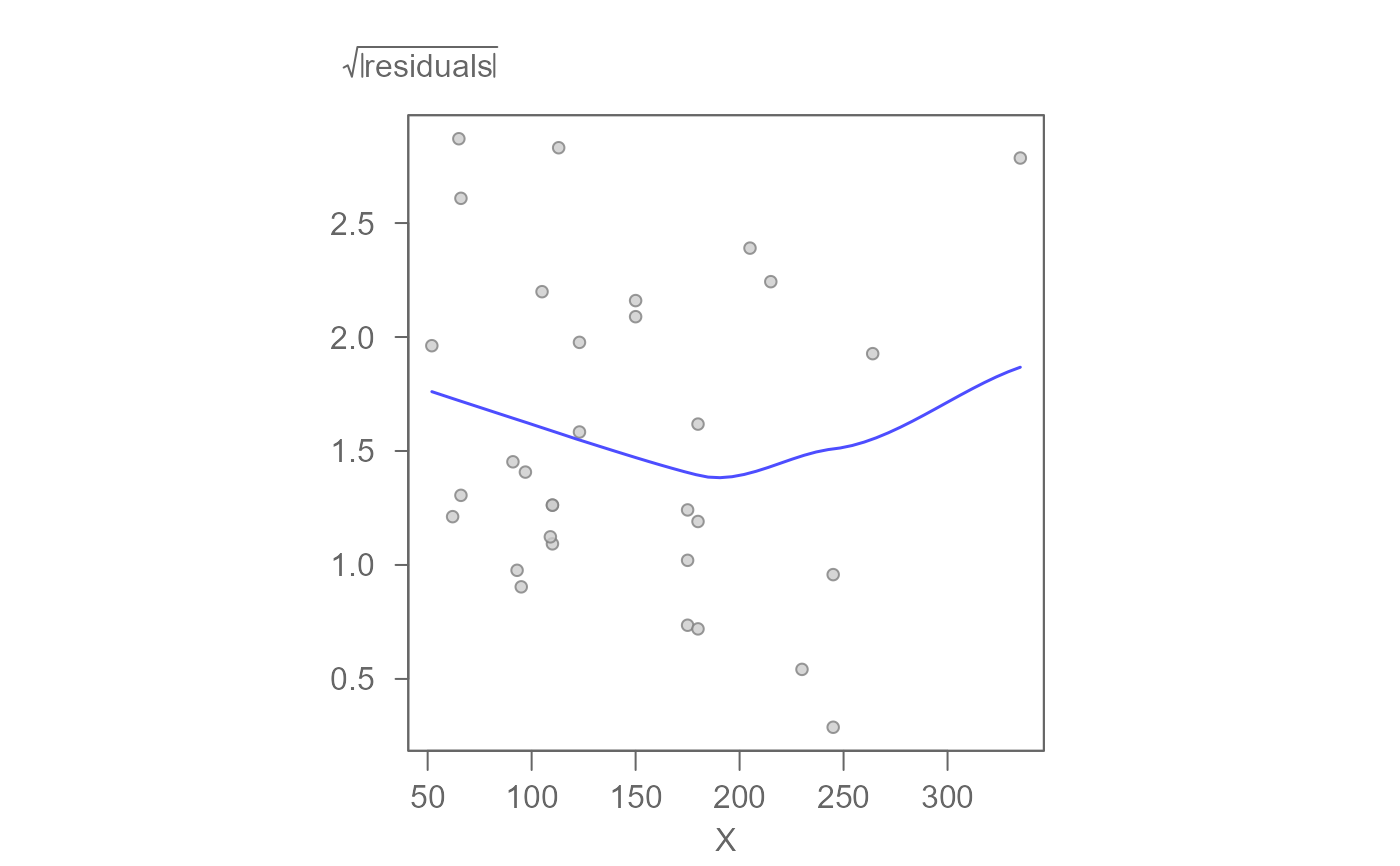
William Cleveland's spread-location plot applied to residuals of a linear model.
\(\ spread = \sqrt{|residuals|}\)
\(\ dependence = x\ variable\)

References

Understanding Robust and Exploratory Data Analysis, Hoaglin, David C., Frederick Mosteller, and John W. Tukey, 1983.
William S. Cleveland. Visualizing Data. Hobart Press (1993)

Examples

cars <- MASS::Cars93
# Cleveland's spread-location plot applied to univariate data
eda_sl(cars, MPG.city, Type)


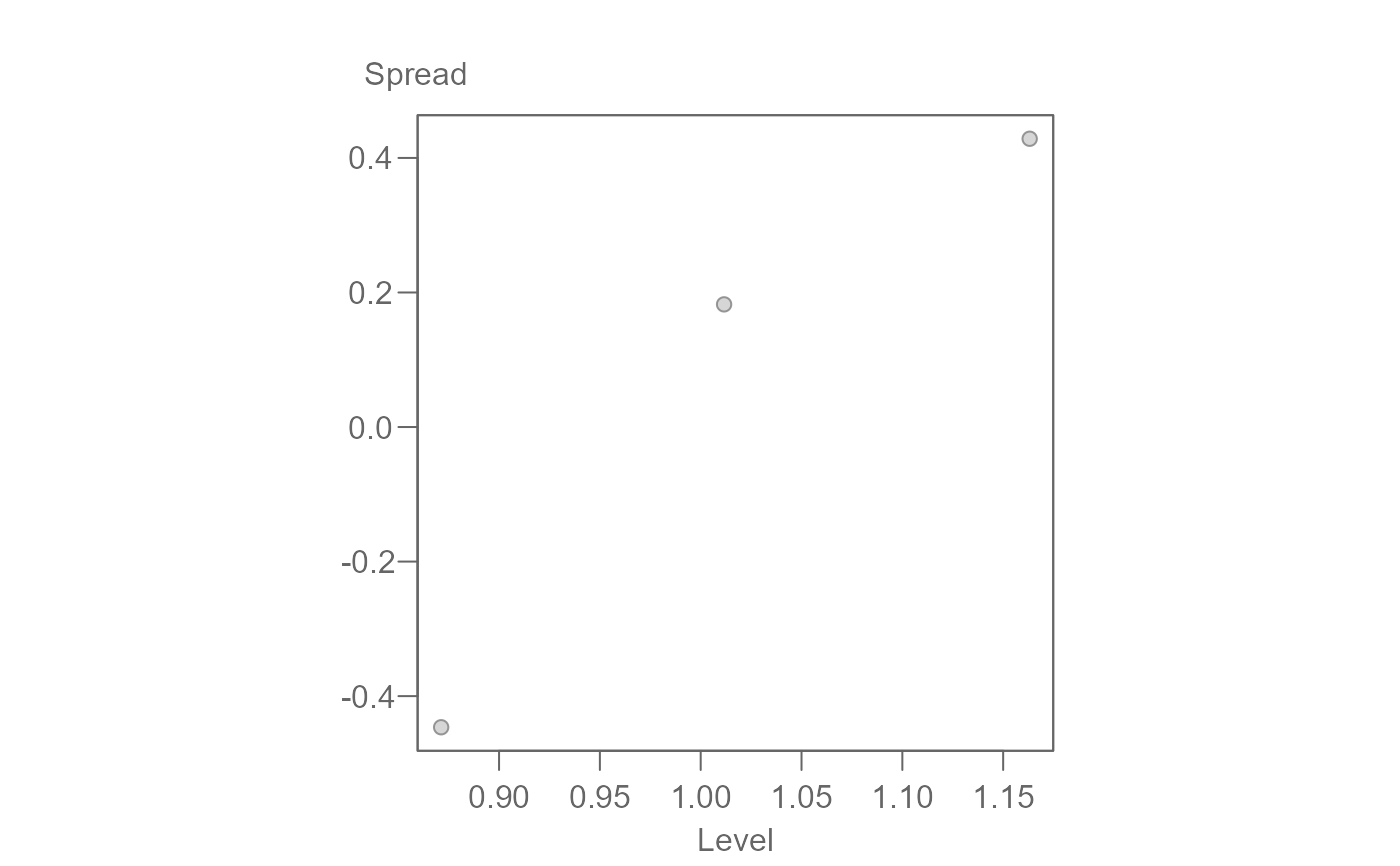# You can specify the exact form of the spread on the y-axis
# via the ylab argument
eda_sl(cars, MPG.city, Type, ylab = expression(sqrt(abs(residuals))) )


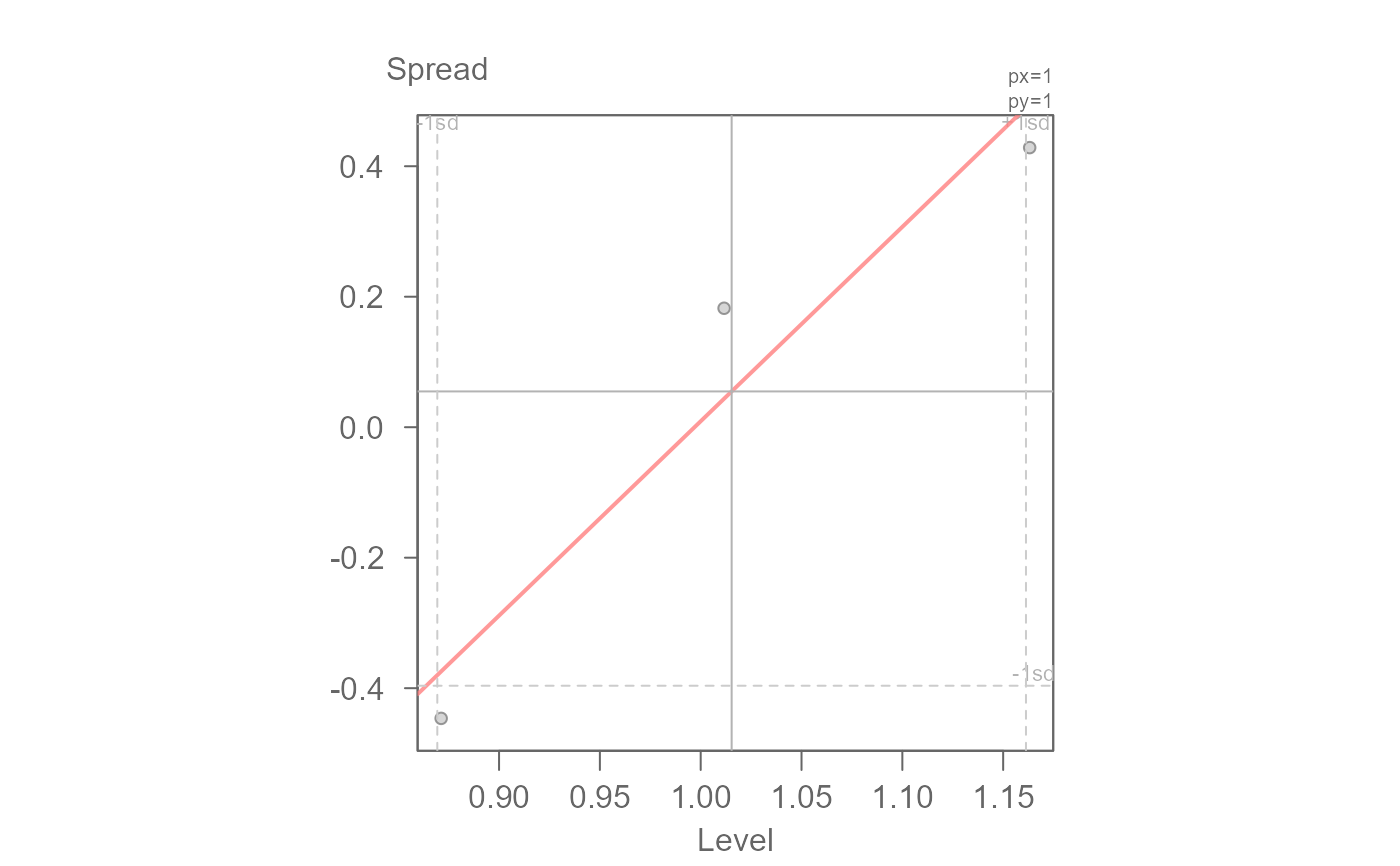# The function can also generate Tukey's spread-level plot to identify a
# power transformation that can stabilize spread across fitted values
# following power = 1 - slope
eda_sl(cars, MPG.city, Type, type = "level")

#>        int Location^1 
#>  -8.009091   2.969832 

# A slope of around 3 is computed from the s-l plot, therefore, a suggested
# power is 1 - 3 = -2. We can apply a power transformation within the
# function via the p argument. By default, a Box-Cox transformation method
# is adopted.
eda_sl(cars, MPG.city, Type, p = -2)


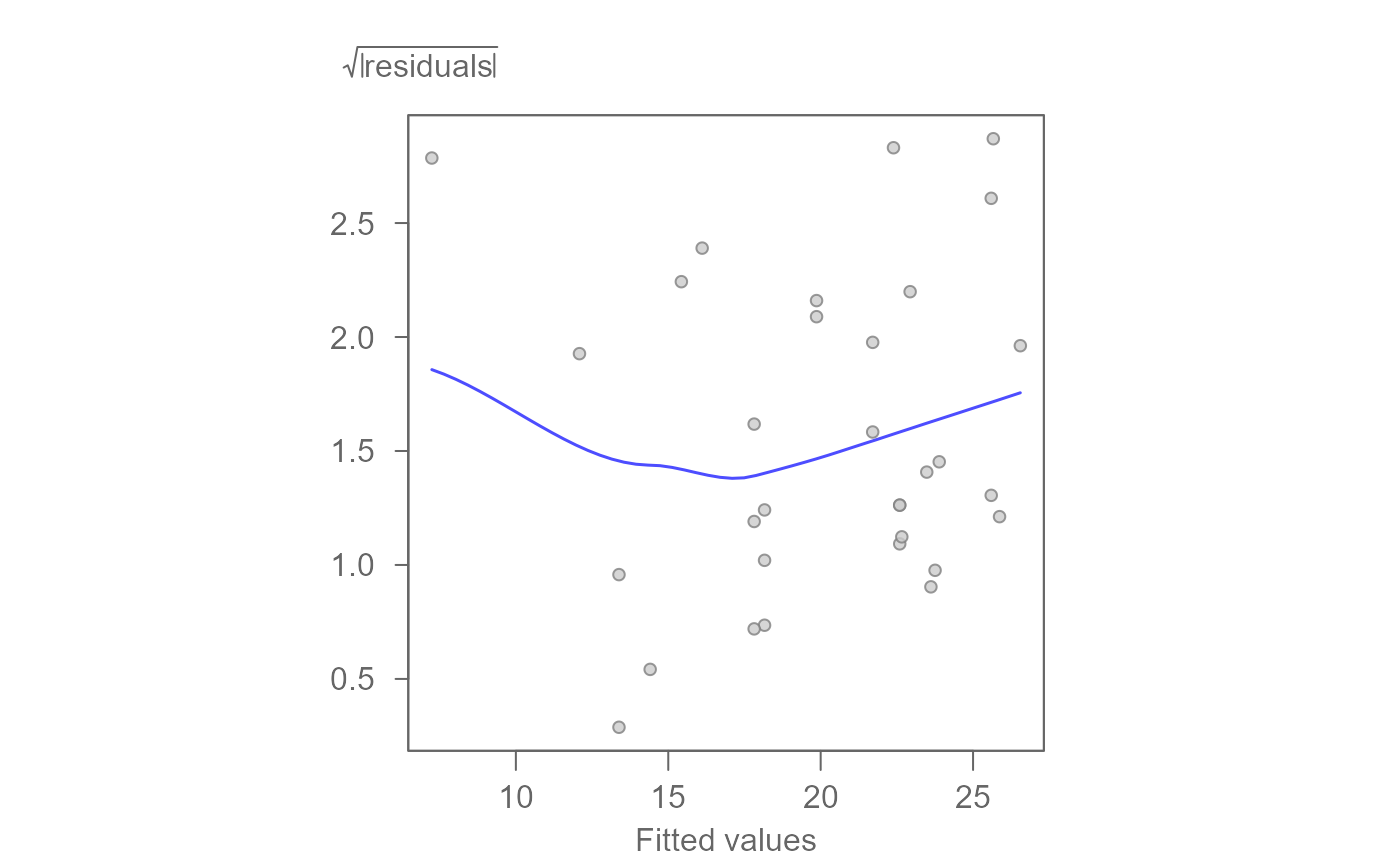
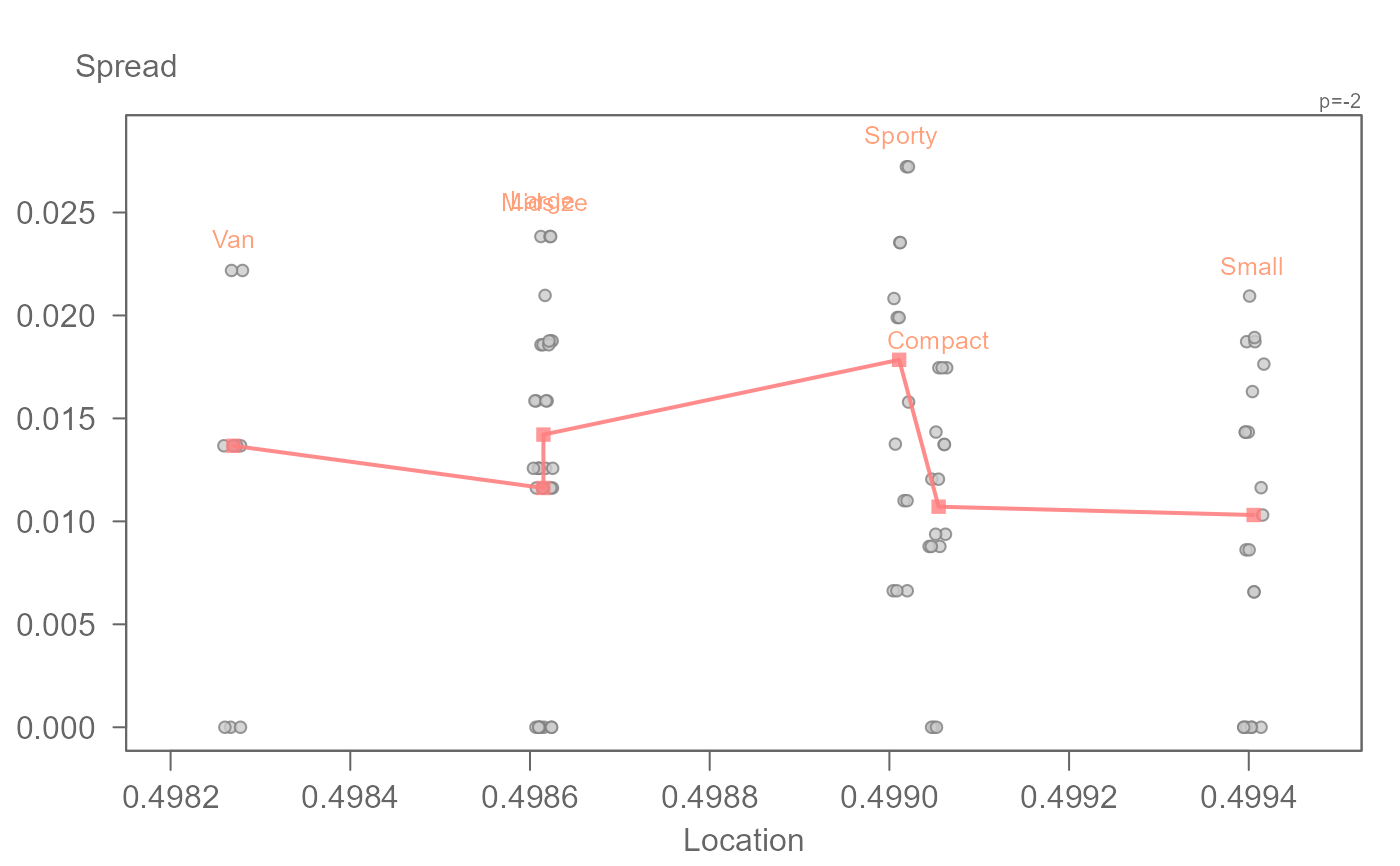# Spread-location plot can also be generated from residuals of a linear model
M1 <- lm(mpg ~ hp, mtcars)
eda_sl(M1)


# Spread can be compared to X instead of fitted value
eda_sl(M1, type = "dependence")