Symmetry QQ plot — eda_sym • tukeyedar

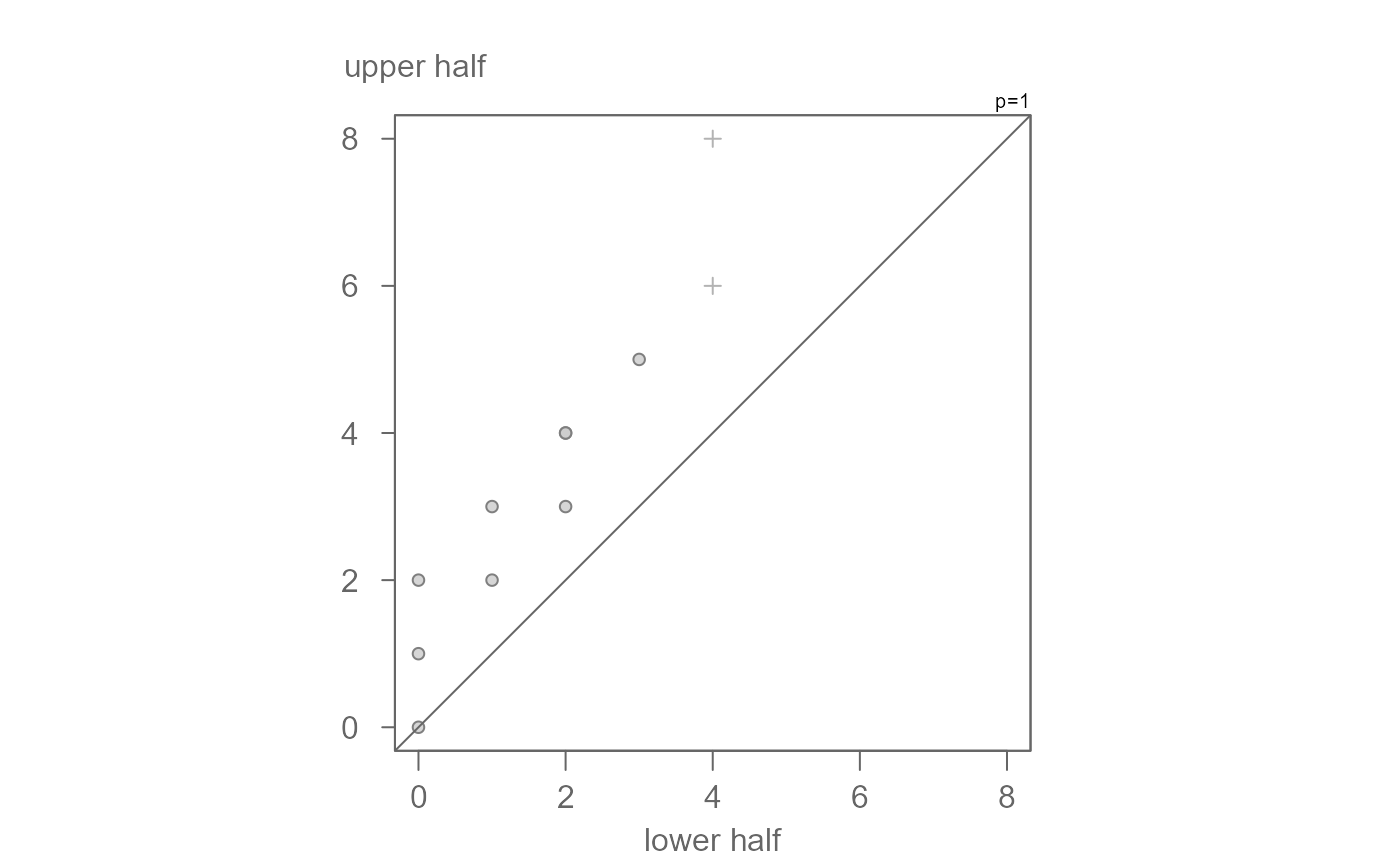
eda_sym Generates a symmetry QQ plot.

Usage

eda_sym(
  x,
  p = 1L,
  tukey = FALSE,
  base = exp(1),
  q.type = 5,
  show.par = TRUE,
  grey = 0.6,
  pch = 21,
  p.col = "grey50",
  p.fill = "grey80",
  size = 0.8,
  alpha = 0.8,
  inner = 0.75,
  q = TRUE,
  qcol = rgb(0, 0, 0, 0.05),
  tails = FALSE,
  tail.pch = 21,
  tail.p.col = "grey70",
  tail.p.fill = NULL,
  xlab = NULL,
  ylab = NULL,
  title = NULL,
  t.size = 1.2,
  plot = TRUE,
  ...
)

Arguments

x: Vector of sample
p: Power transformation to apply to x.
tukey: Boolean determining if a Tukey transformation should be adopted (FALSE adopts a Box-Cox transformation).
base: Base used with the log() function if px or py is 0.
q.type: An integer between 1 and 9 selecting one of the nine quantile algorithms used to generate inner shaded region. (See quantiletile function).
show.par: Boolean determining if power parameter should be displayed.
grey: Grey level to apply to plot elements (0 to 1 with 1 = black).
pch: Point symbol type.
p.col: Color for point symbol.
p.fill: Point fill color passed to bg (Only used for pch ranging from 21-25).
size: Point size (0-1)
alpha: Point transparency (0 = transparent, 1 = opaque). Only applicable if rgb() is not used to define point colors.
inner: Fraction of the input data considered as "mid values". Defaults to 75\ which of the tail-end points are to be symbolized differently, tails.
q: Boolean determining if inner data region should be shaded.
qcol: Fill color of inner quantile box.
tails: Boolean determining if points outside of the inner region should be symbolized differently. Tail-end points are symbolized via the tail.pch, tail.p.col and tail.p.fill arguments.
tail.pch: Tail-end point symbol type (See tails).
tail.p.col: Tail-end color for point symbol (See tails).
tail.p.fill: Tail-end point fill color passed to bg (Only used for tail.pch ranging from 21-25).
xlab: X label for output plot. Ignored if x is a dataframe.
ylab: Y label for output plot. Ignored if x is a dataframe.
title: Title to add to plot.
t.size: Title size.
plot: Boolean determining if plot should be generated.
...: Not used

Value

Returns a dataframe of upper and lower halves

Details

Generates a symmetry quantile plot that compares the lower half of the sorted data to its upper half. If the distribution is perfectly symmetrical, the points will fall on the line.

References

John M. Chambers, William S. Cleveland, Beat Kleiner, Paul A. Tukey. Graphical Methods for Data Analysis (1983)
Symmetry quantile plot article

Examples


 singer <- lattice::singer
 tenor1 <- subset(singer, voice.part == "Tenor 1", select = height, drop = TRUE )
 
 # Default plot
 eda_sym(tenor1)

 
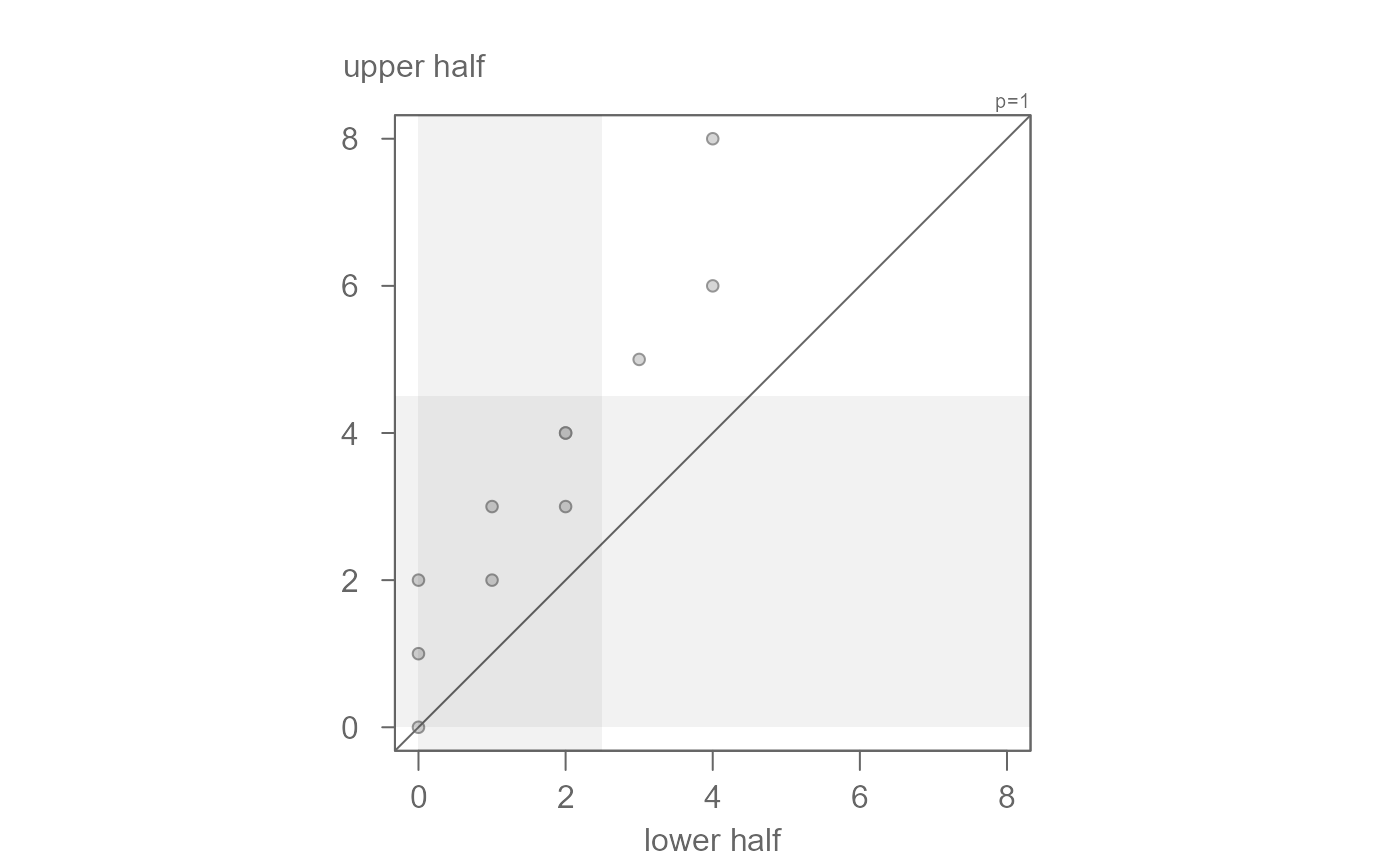 # To remove inner region grey box set q to FALSE
 eda_sym(tenor1, q = FALSE)

 
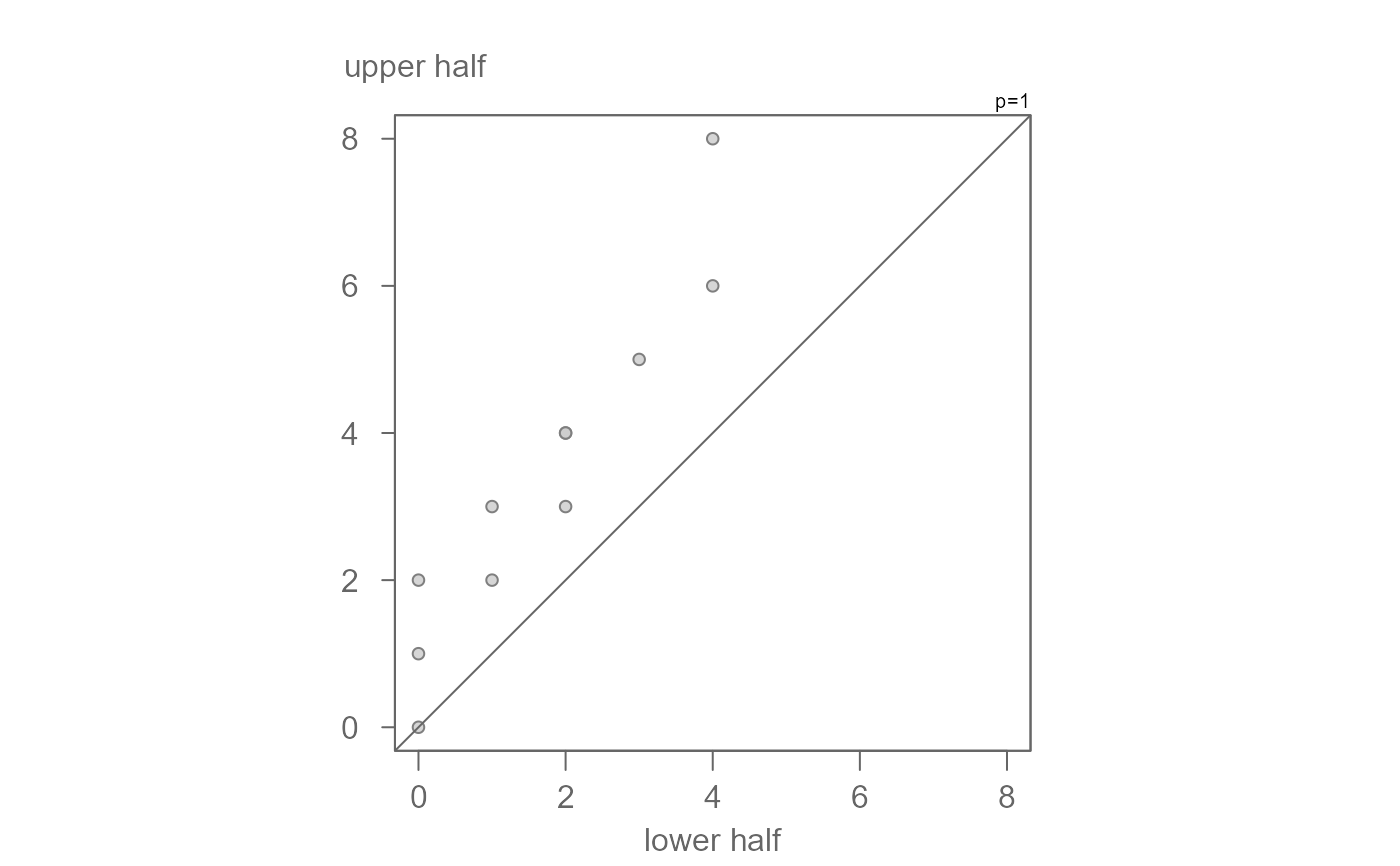 # You can also choose to have the points outside of the inner region
 # symbolized differently
 eda_sym(tenor1, q = FALSE, tails = TRUE, tail.pch = 3)