Skip to contents

Tukey's resistant line

Source: R/eda_rline.R
eda_rline.Rd

eda_rline is an R implementation of Hoaglin, Mosteller and Tukey's resistant line technique outlined in chapter 5 of "Understanding Robust and Exploratory Data Analysis" (Wiley, 1983).

Usage

eda_rline(
  dat,
  x,
  y,
  px = 1,
  py = 1,
  tukey = FALSE,
  maxiter = 20,
  base = exp(1)
)

Arguments

dat

Data frame.

x

Column assigned to the x axis.

y

Column assigned to the y axis.

px

Power transformation to apply to the x-variable.

py

Power transformation to apply to the y-variable.

tukey

Logical; determining if a Tukey transformation should be adopted. (FALSE adopts a Box-Cox transformation).

maxiter

Maximum number of iterations to run.

base

Base used with the log() function if px or py is 0.

Value

Returns a list of class eda_rline with the following named components:

  • data: Input data table with residuals

  • a: Intercept

  • b: Slope

  • residuals: Residuals sorted on x-values

  • x: Sorted x values

  • y: y values following sorted x-values

  • xmed: Median x values for each third

  • ymed: Median y values for each third

  • index: Index of sorted x values defining upper boundaries of each thirds

  • xlab: X label name

  • ylab: Y label name

  • iter: Number of iterations

  • fitted.values: Fitted values

Details

This is an R implementation of the RLIN.F FORTRAN code in Velleman et. al's book. This function fits a robust line using a three-point summary strategy whereby the data are split into three equal length groups along the x-axis and a line is fitted to the medians defining each group via an iterative process. This function should mirror the built-in stat::line function in its fitting strategy but it outputs additional parameters.


See the accompanying resistant line article for a detailed breakdown of the resistant line technique.

References

  • Velleman, P. F., and D. C. Hoaglin. 1981. Applications, Basics and Computing of Exploratory Data Analysis. Boston: Duxbury Press.

  • D. C. Hoaglin, F. Mosteller, and J. W. Tukey. 1983. Understanding Robust and Exploratory Data Analysis. Wiley.

See also

plot.eda_rline()

Examples


# This first example uses breast cancer data from "ABC's of EDA" page 127.
# The output model's  parameters should closely match:  Y = -46.19 + 2.89X
# The plots shows the original data with a fitted resistant line (red)
# and a regular lm fitted line (dashed line), and the modeled residuals.
# The 3-point summary dots are shown in red.

M <- eda_rline(neoplasms, Temp, Mortality)
M
#> $data
#>    Temp Mortality    residuals
#> 1  31.8      67.3  21.59489403
#> 2  34.0      52.5   0.43651252
#> 3  40.2      68.1  -1.88256262
#> 4  42.1      84.6   9.12610790
#> 5  42.3      65.1 -10.95192678
#> 6  43.5      72.2  -7.32013487
#> 7  44.2      81.7   0.15674374
#> 8  45.1      89.2   5.05558767
#> 9  46.3      78.9  -8.71262042
#> 10 47.3      88.6  -1.90279383
#> 11 47.8      95.0   3.05211946
#> 12 48.5      87.0  -6.97100193
#> 13 49.2      95.9  -0.09412331
#> 14 49.9     104.5   6.48275530
#> 15 50.0     100.4   2.09373796
#> 16 51.3     102.5   0.43651252
#> 
#> $b
#> [1] 2.890173
#> 
#> $a
#> [1] -46.20241
#> 
#> $residuals
#>  [1]  21.59489403   0.43651252  -1.88256262   9.12610790 -10.95192678
#>  [6]  -7.32013487   0.15674374   5.05558767  -8.71262042  -1.90279383
#> [11]   3.05211946  -6.97100193  -0.09412331   6.48275530   2.09373796
#> [16]   0.43651252
#> 
#> $x
#>  [1] 31.8 34.0 40.2 42.1 42.3 43.5 44.2 45.1 46.3 47.3 47.8 48.5 49.2 49.9 50.0
#> [16] 51.3
#> 
#> $y
#>  [1]  67.3  52.5  68.1  84.6  65.1  72.2  81.7  89.2  78.9  88.6  95.0  87.0
#> [13]  95.9 104.5 100.4 102.5
#> 
#> $xmed
#> [1] 40.2 45.7 49.9
#> 
#> $ymed
#> [1]  67.30  85.15 100.40
#> 
#> $index
#> [1]  5 11 16
#> 
#> $xlab
#> [1] "Temp"
#> 
#> $ylab
#> [1] "Mortality"
#> 
#> $px
#> [1] 1
#> 
#> $py
#> [1] 1
#> 
#> $tukey
#> [1] FALSE
#> 
#> $base
#> [1] 2.718282
#> 
#> $iter
#> [1] 4
#> 
#> $fitted.values
#>  [1]  45.70511  52.06349  69.98256  75.47389  76.05193  79.52013  81.54326
#>  [8]  84.14441  87.61262  90.50279  91.94788  93.97100  95.99412  98.01724
#> [15]  98.30626 102.06349
#> 
#> attr(,"class")
#> [1] "eda_rline"

# Plot the output (red line is the resistant line)
plot(M)


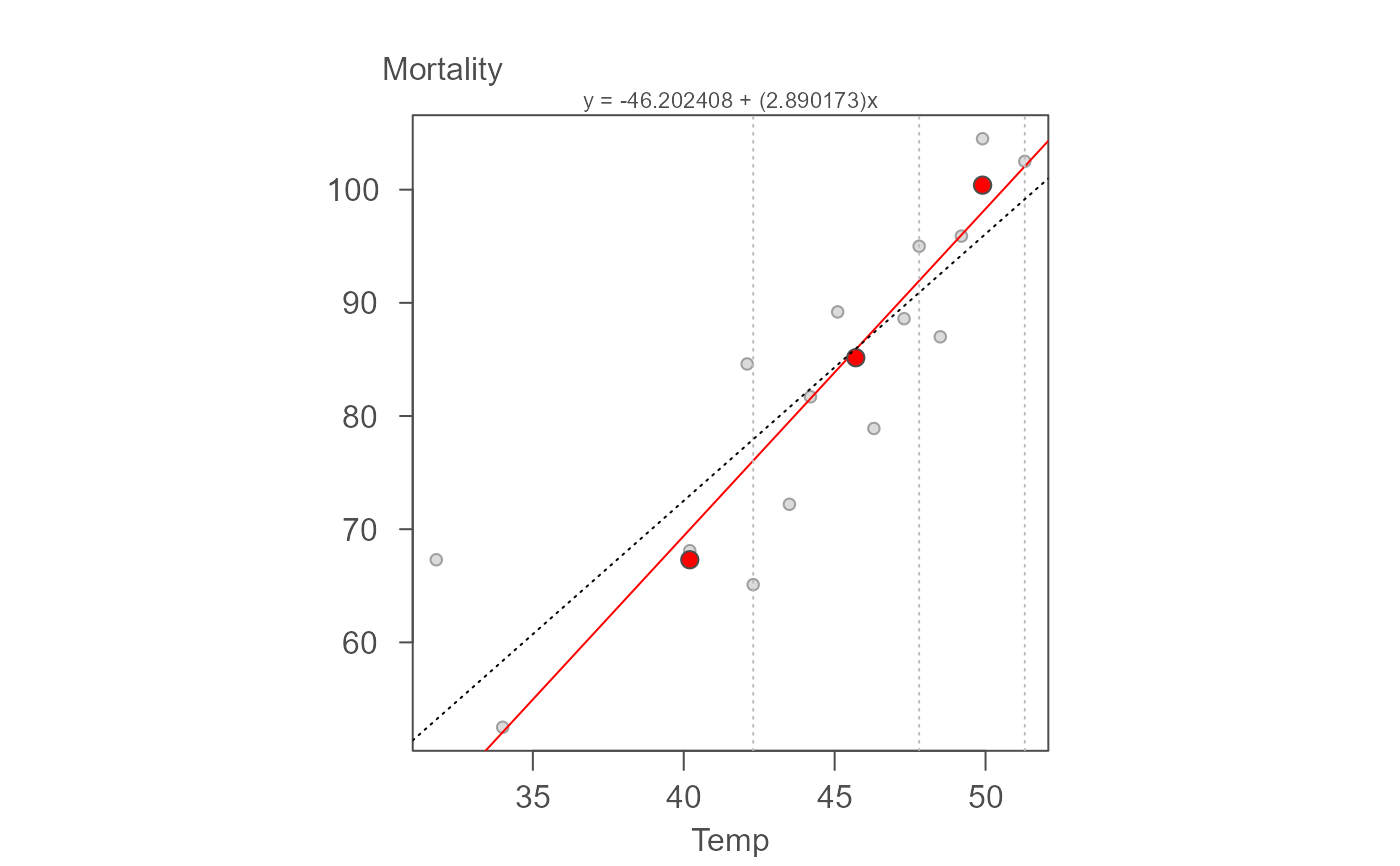# Add a traditional OLS regression line (dashed blue line)
plot(M, reg = TRUE)

#>        int     Temp^1 
#> -21.794691   2.357695 

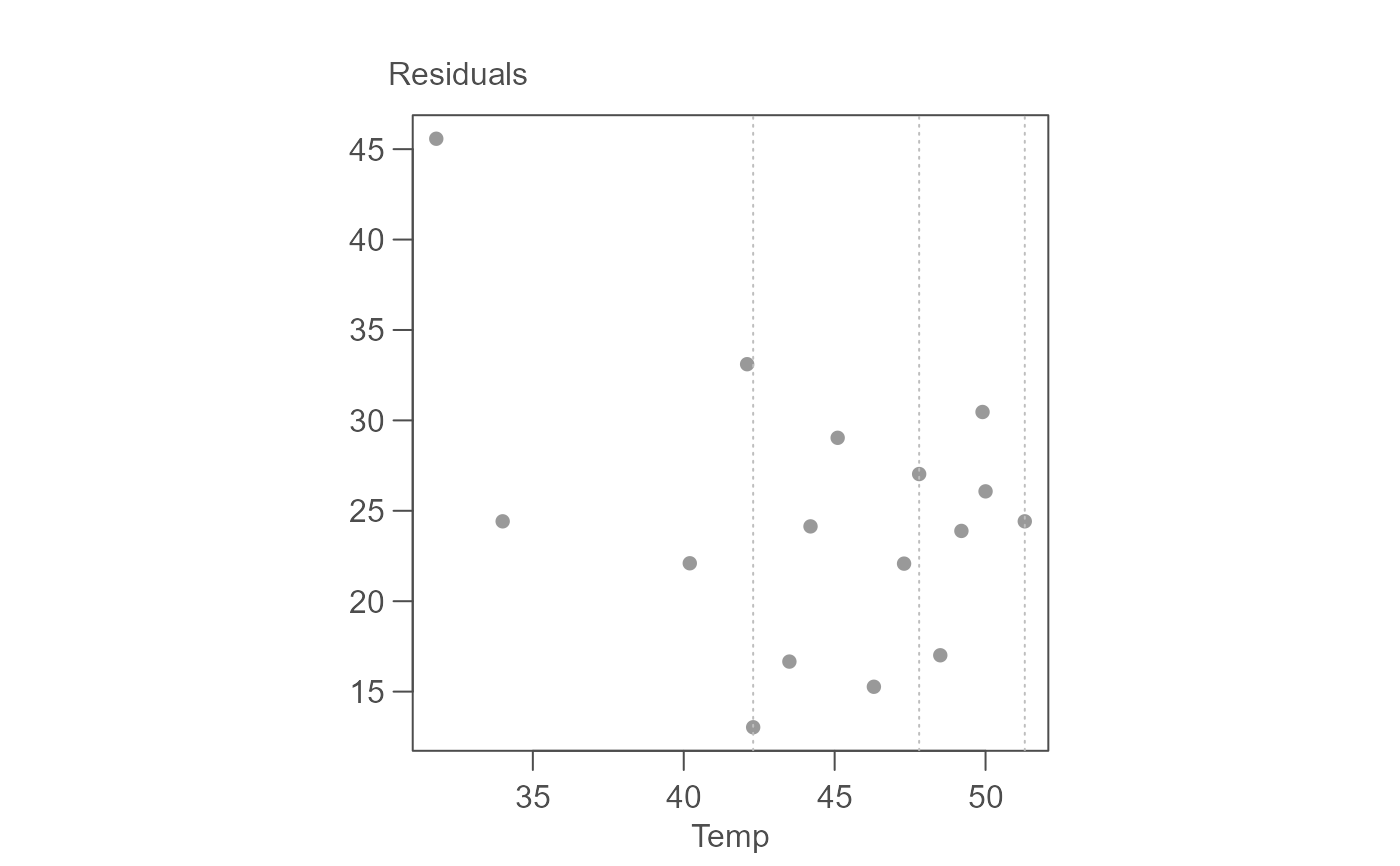
# Plot the residuals
plot(M, plot = "residuals")


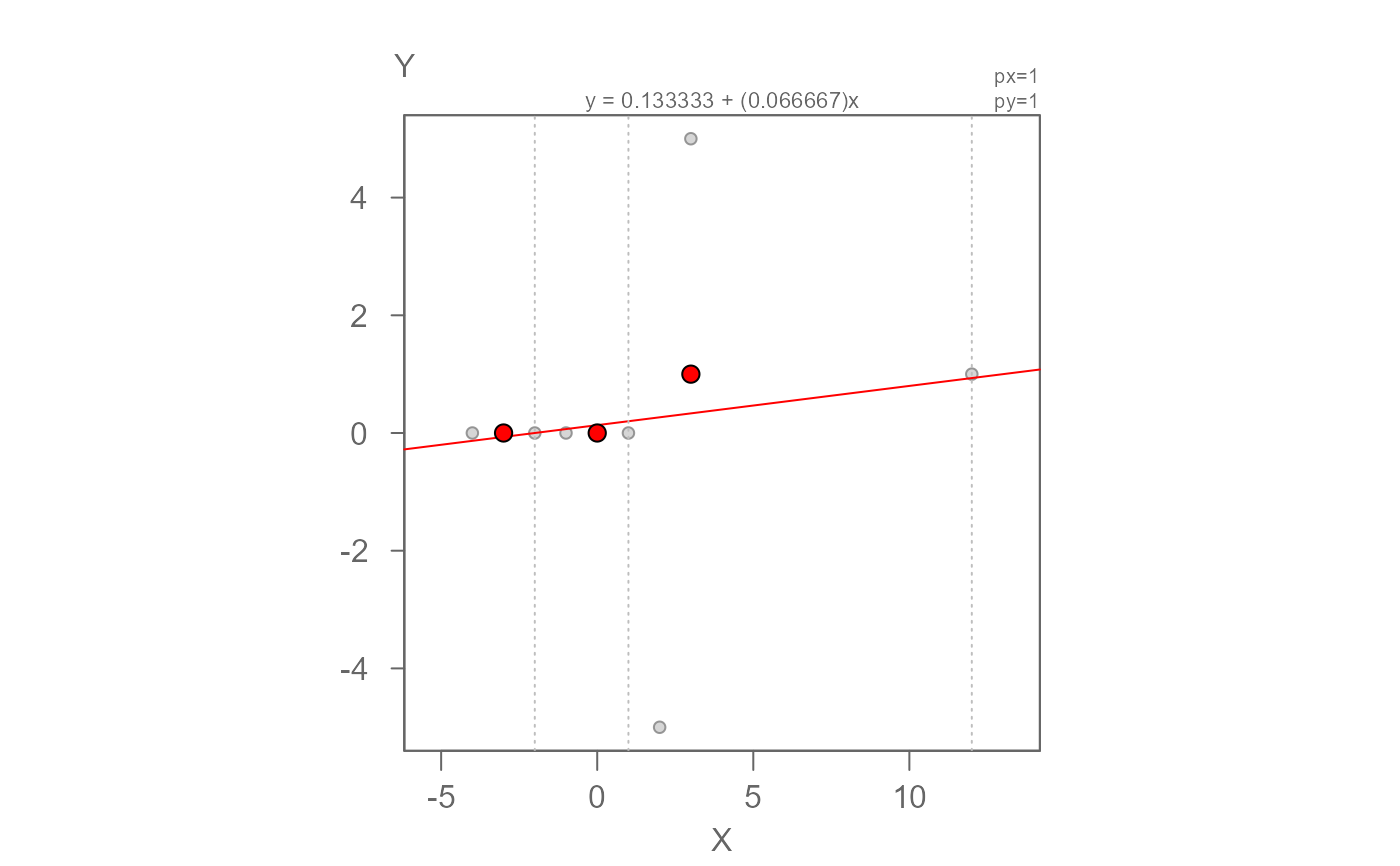
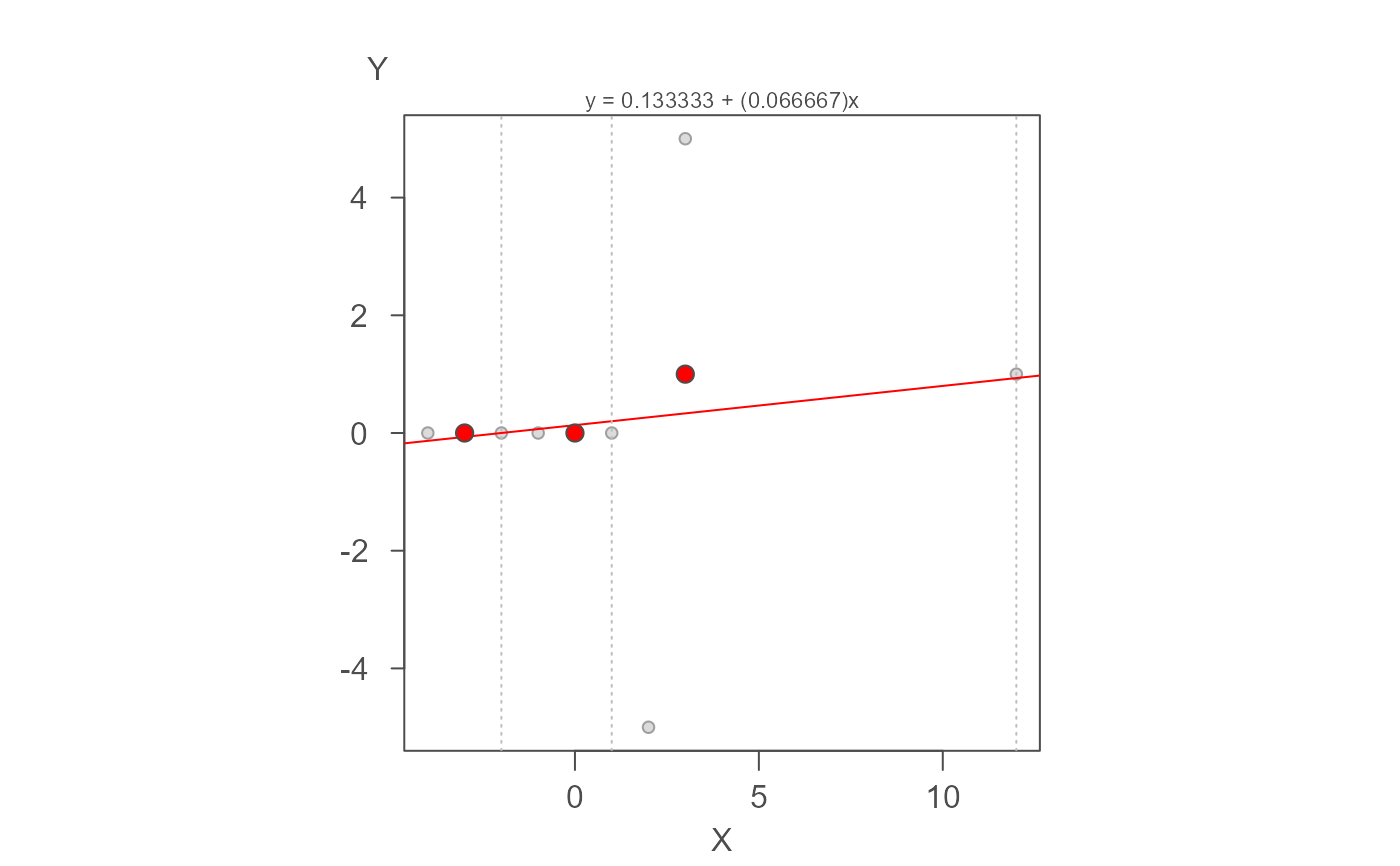# This next example uses Andrew Siegel's pathological 9-point dataset to test
# for model stability when convergence cannot be reached.
M <- eda_rline(nine_point, X, Y)
plot(M)