Chapter 13 Spatial Autocorrelation

13.1 Introduction

In the previous chapter, we explored how polynomial functions can be used to model spatial trends that capture broad, location-driven variation in continuous spatial fields. By fitting and removing global trends, we revealed residuals that may still exhibit spatial structure. This chapter builds on that foundation by introducing spatial autocorrelation, a second-order property that describes how values at one location relate to values at nearby locations.

This concept is rooted in Tobler’s First Law of Geography which states:

“The first law of geography: Everything is related to everything else, but near things are more related than distant things.” Waldo R. Tobler (Tobler 1970)

This principle underpins much of spatial analysis. It suggests that spatial data often exhibit non-random patterns, where nearby features tend to have similar attribute values. Spatial autocorrelation provides a formal way to quantify this tendency.

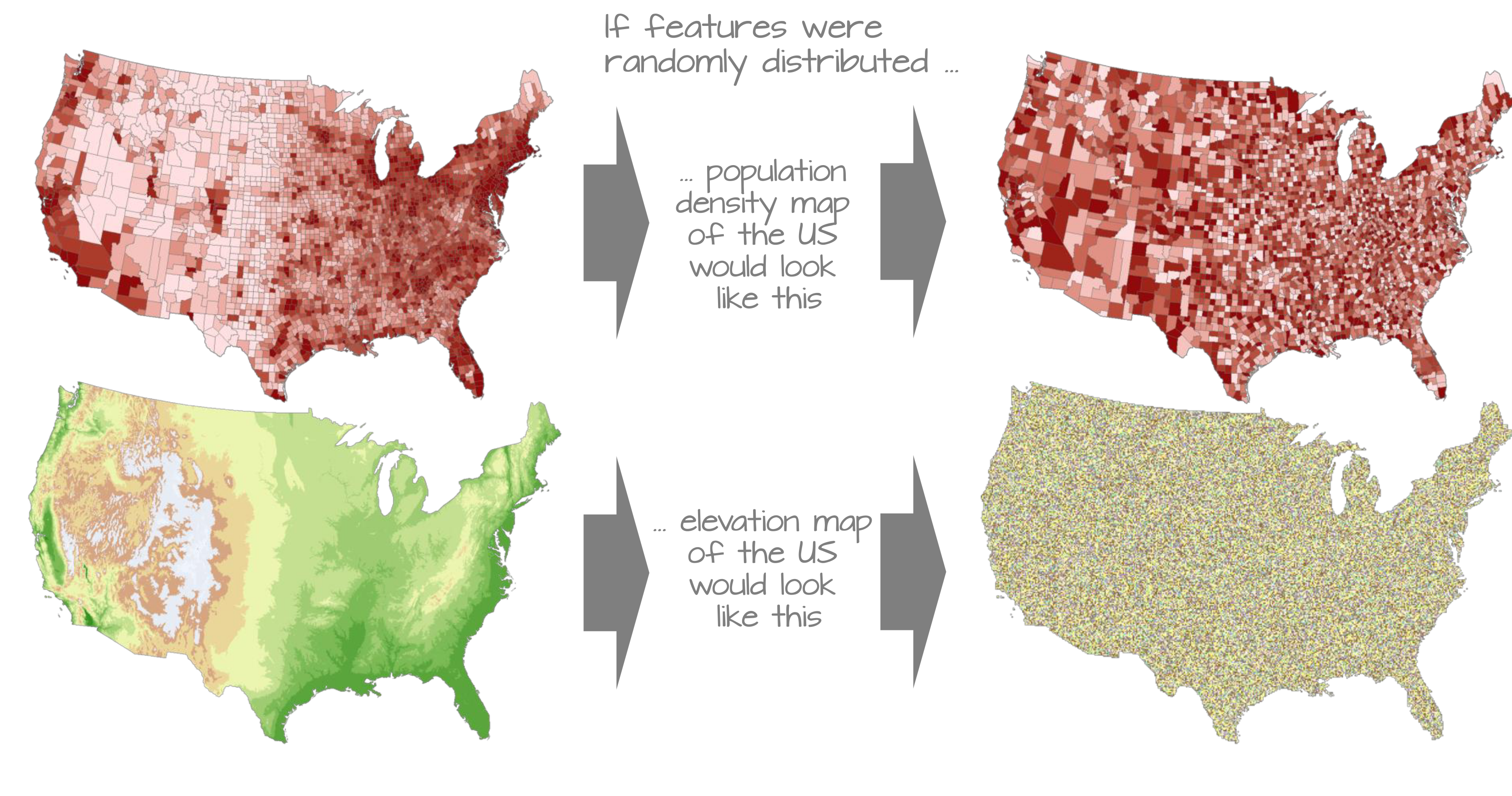
To make the mathematical foundations of autocorrelation more accessible, we shift from the raster-based data used in the previous chapter to a simpler dataset composed of polygonal areal units (e.g., counties). This allows us to clearly illustrate how spatial relationships are defined, how spatial weights are constructed, and how measures like Moran’s I are computed.

This chapter focuses on:

• Defining spatial autocorrelation and its role in spatial statistics.
• Constructing spatial weights to represent neighborhood relationships.
• Computing and interpreting global and local Moran’s I statistics.
• Using permutation-based hypothesis testing to assess significance.

13.2 Global Moran’s I

While maps can sometimes reveal clusters of similar values, our visual interpretation is often limited, especially when patterns are subtle or complex. To move beyond subjective impressions, we need a quantitative and objective measure of spatial patterning. Specifically, we want to quantify the degree to which similar attribute values are clustered or dispersed across space.

One widely used statistic for this purpose is Moran’s I , a measure of global spatial autocorrelation. It quantifies the overall tendency for features with similar values to be located near one another, based on a defined spatial relationship (e.g., contiguity or distance). In essence, Moran’s I is a correlation coefficient between a variable and its spatially lagged counterpart.

13.2.1 Computing the Moran’s I

Let’s start with a working example: 2020 median per capita income for the state of Maine.

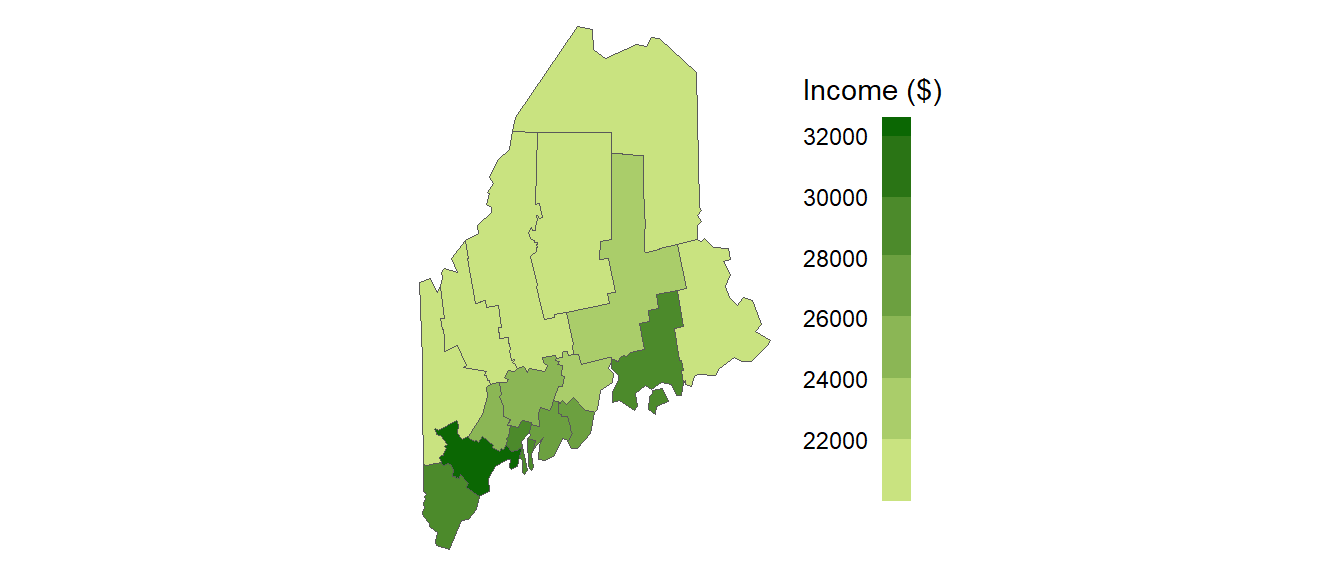
Figure 13.1: Map of 2020 median per capita income for Maine counties (USA).

It may seem apparent that, when aggregated at the county level, the income distribution appears clustered with high counties surrounded by high counties and low counties surrounded by low counties (note that we are ignoring potential first-order trends here for pedagogical clarity; a spatial trend model could have been discerned). But a qualitative description may not be sufficient; we might want to quantify the degree to which similar (or dissimilar) counties are clustered. One measure of this type of relationship is the Moran’s I statistic.

The Moran’s I statistic is a measure of spatial autocorrelation that quantifies the degree to which similar values (like income) cluster together in space. It is computed as the correlation between a variable and its spatially lagged counterpart, based on a defined spatial weights matrix.

But before we go about computing this correlation, we need to come up with a way to define a neighbor. One approach is to define a neighbor as being any contiguous polygon. For example, the northern most county (Aroostook), has four contiguous neighbors while the southern most county (York) has just two contiguous counties. Other neighborhood definitions can include distance bands (e.g. counties within 100 km) and k nearest neighbors (e.g. the 2 closest neighbors). Note that distance bands and k nearest neighbors are usually measured using the polygon’s centroids and not their boundaries.

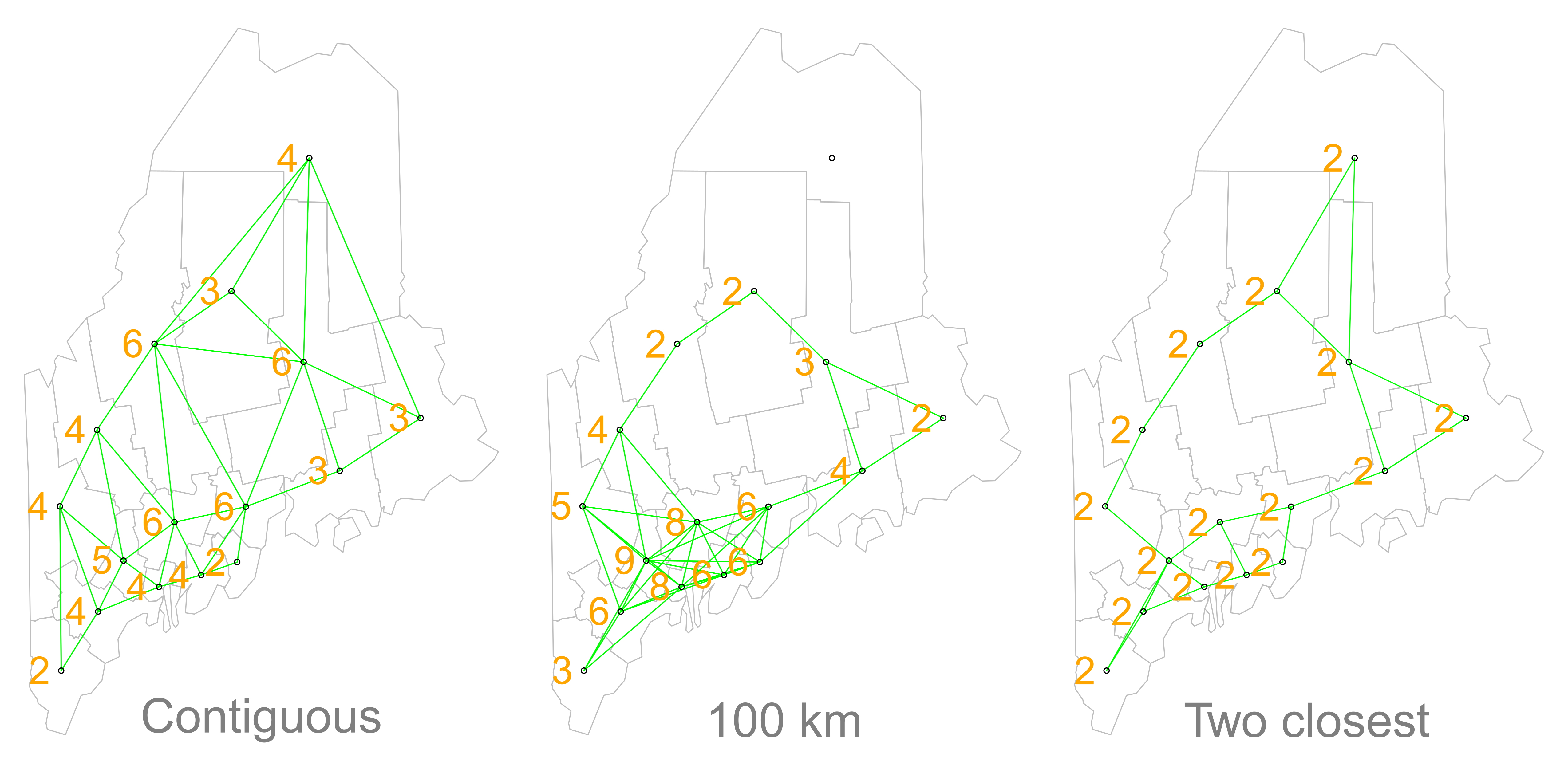
Figure 13.2: Maps show the links between each polygon and their respective neighbor(s) based on the neighborhood definition. A contiguous neighbor is defined as one that shares a boundary or a vertex with the polygon of interest. Orange numbers indicate the number of neighbors for each polygon. Note that the top most county has no neighbors when a neighborhood definition of a 100 km distance band is used (i.e. no centroids are within a 100 km search radius)

Once we’ve defined a neighborhood for our analysis, we identify the neighbors for each polygon in our dataset then summaries the values for each neighborhood cluster (by computing their mean values, for example). This summarized neighborhood value is sometimes referred to as a spatially lagged value (X_lag). In our working example, we adopt a contiguity neighborhood and compute the average neighboring income value (Income_lag) for each county in our dataset. We then plot Income_lag against Income for each county. The Moran’s I coefficient between Income_lag and Income is nothing more than the slope of the least squares regression line that best fits the points after standardizing both variables (i.e., converting them to z-scores), which centers them on the mean and scales them by their standard deviation.

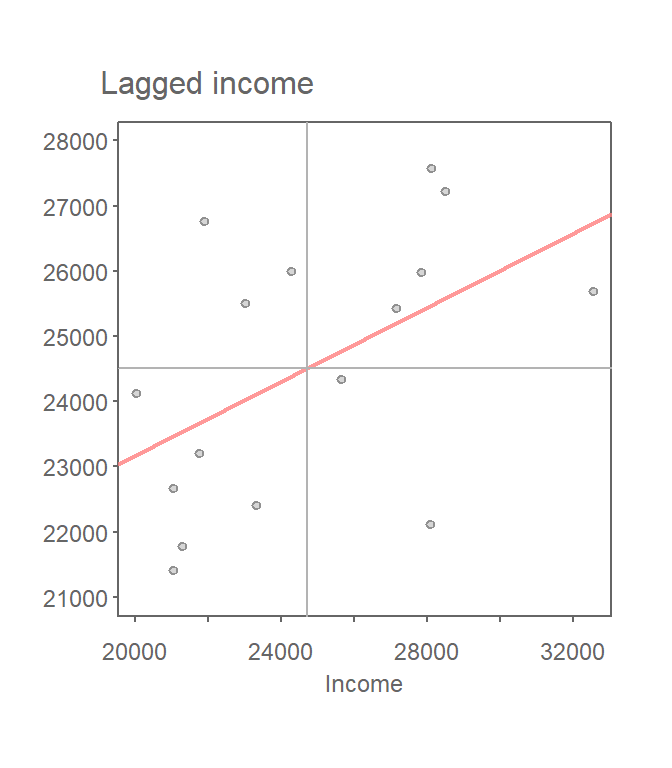
Figure 13.3: Scatter plot of spatially lagged income (neighboring income) vs. each countie’s income. If we equalize the spread between both axes (i.e. convert to a z-value) the slope of the regression line represents the Moran’s I statistic.

If there is no degree of association between Income and Income_lag, the slope will be close to flat (resulting in a Moran’s I value near 0). In our working example, the slope is far from flat with a Moran’s I value of 0.28. So this raises the question: how significant is this Moran’s I value (i.e. is the computed slope significantly different from 0)? There are two approaches to estimating the significance: an analytical solution and a Monte Carlo solution. The analytical solution makes some restrictive assumptions about the data and thus cannot always be reliable. The other approach (and the one favored here) is a Monte Carlo test. This approach avoids parametric assumptions about the data distribution or spatial layout, relying instead on the assumption that values are exchangeable under the null hypothesis.

13.2.2 Monte Carlo approach to estimating significance

In a Monte Carlo test (specifically, a permutation-based bootstrap test) we assess the significance of an observed Moran’s I statistic by comparing it to a distribution of values generated under the null hypothesis of spatial randomness. This is done by permuting the attribute values across spatial units while keeping the spatial structure (e.g., neighborhood relationships) fixed.

For each permutation, the attribute values are shuffled among the polygons and a new Moran’s I value is computed.

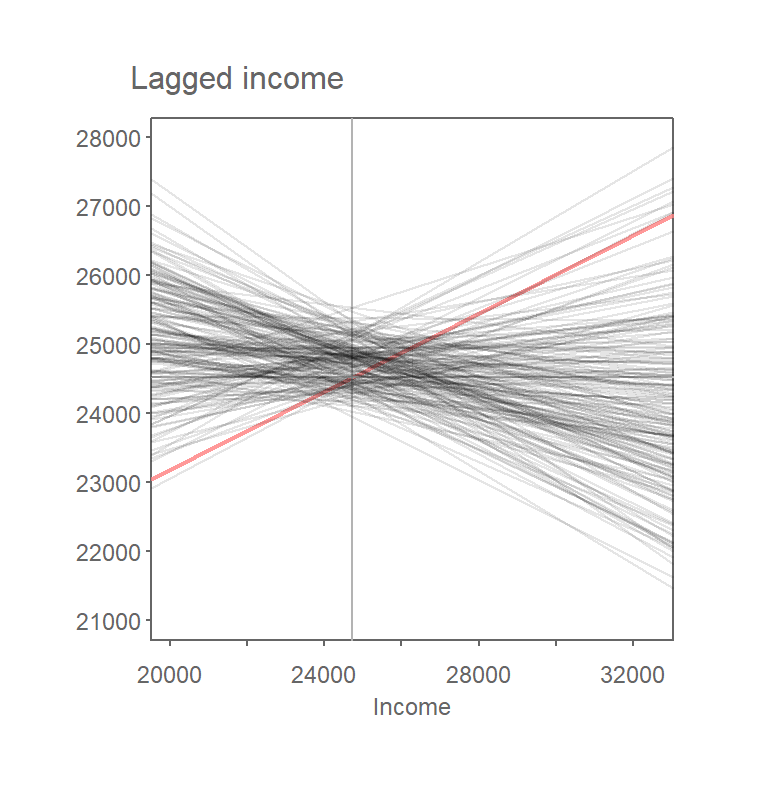
Figure 13.4: Results from 199 permutations. Plot shows Moran’s I lines (in gray) computed from each random permutation of income values. The observed Moran’s I line for the original dataset is shown in red.

Repeating this process many times yields a sampling distribution of Moran’s I values that would be expected if the observed values were randomly distributed across space.

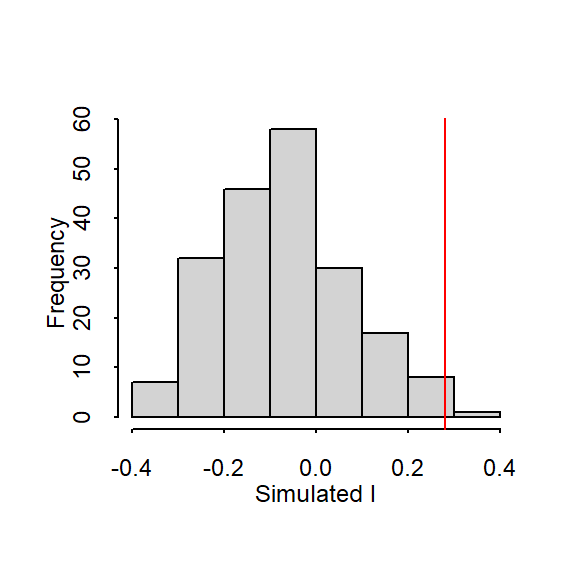
Figure 13.5: Histogram shows the distribution of Moran’s I values for all 199 permutations; red vertical line shows our observed Moran’s I value of 0.28.

In our working example, 199 simulations indicate that our observed Moran’s I value of 0.28 is not a value we would expect to compute if the income values were randomly distributed across each county. A pseudo p-value can easily be computed from the simulation results:

\[ \dfrac{N_{extreme}+1}{N+1} \]

where \(N_{extreme}\) is the number of simulated Moran’s I values more extreme than our observed statistic and \(N\) is the total number of simulations. Here, out of 199 simulations, just three simulated I values were more extreme than our observed statistic, \(N_{extreme}\) = 3, so \(p\) is equal to (3 + 1) / (199 + 1) = 0.02. This is interpreted as “there is a 2% probability that we would be wrong in rejecting the null hypothesis H_o.”

Note that in this permutation example, we shuffled the observed income values among polygons without replacement–this is referred to as a permutation-based randomization. This should not be confused with distribution-based simulation where new values are randomly generated from a theoretical distribution and assigned to features.

Alternatively, one can choose to randomly assign a set of values to each feature in a data layer from a theorized distribution (for example, a Normal distribution). This may result in a completely different set of values for each permutation outcome. Note that you would only adopt this approach if the theorized distribution underpinning the value of interest is known a priori.

Another important consideration when computing a permutation-based p-value from a permutation test is the number of simulations to perform. In the above example we ran 199 permutations, thus, the smallest p-value we could possibly come up with is 1 / (199 + 1) or a p-value of 0.005. You should therefore chose a number of permutations, \(N\), large enough to allow for finer resolution of p-values and more robust inference.

13.3 Moran’s I at different distance bands

So far we have looked at spatial autocorrelation where we define neighbors as all polygons sharing a boundary with the polygon of interest. We may also be interested in studying the ranges of autocorrelation values as a function of distance. The steps for this type of analysis are straightforward:

1. Define a neighborhood structure based on a specific distance band

2. Compute lagged values for the defined set of neighbors.

3. Calculate the Moran’s I value for the defined neighborhood.

4. Repeat for additional distance bands to observe how autocorrelation changes with spatial scale.

For example, the Moran’s I values for income distribution in the state of Maine at distances of 75, 125, up to 325 km are presented in the following plot:

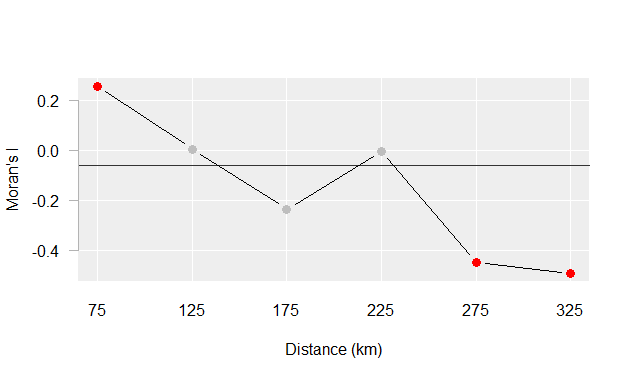
Figure 13.6: Moran’s I at different spatial lags defined by a 50 km width annulus at 50 km distance increments. Red dots indicate Moran I values for which a P-value was 0.05 or less.

The plot suggests that there is significant spatial autocorrelation between counties within 75 km of one another, but as the distances between counties increases, autocorrelation shifts from positive to negative, indicating that nearby counties tend to have similar income levels, while counties farther apart tend to be more dissimilar.

13.4 Local Moran’s I

We can decompose the global Moran’s I into a localized measure of autocorrelation–i.e. a map of “hot spots” and “cold spots”.

A local Moran’s I analysis is best suited for relatively large datasets, especially if a hypothesis test is to be implemented. We’ll therefore switch to another dataset: Massachusetts (USA) household income data aggregated at the U.S. Census’ county subdivision level (as with the Maine dataset, we ignore potential first-order trends here for pedagogical clarity).

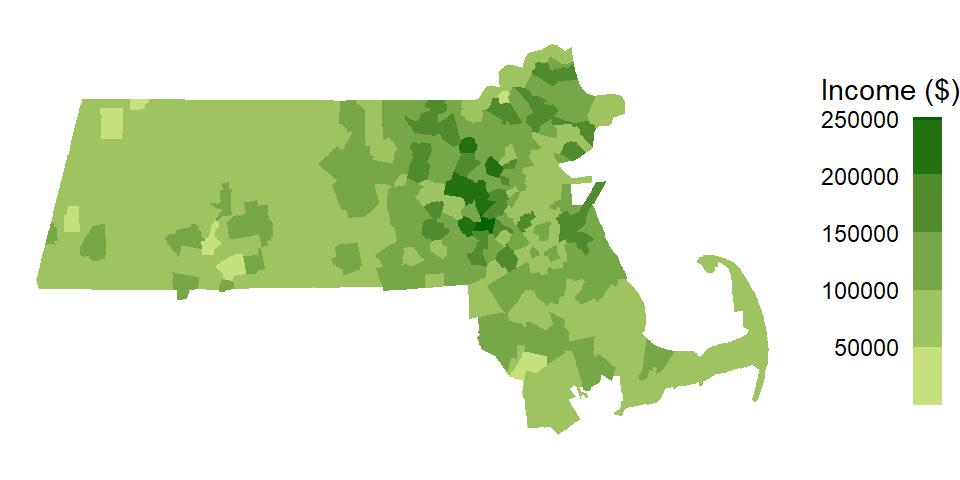
Figure 13.7: Map of 2020 median household income for Massachusetts county subdivisions.

Applying a contiguity based definition of a neighbor, we get the following scatter plot of spatially lagged income vs. income.

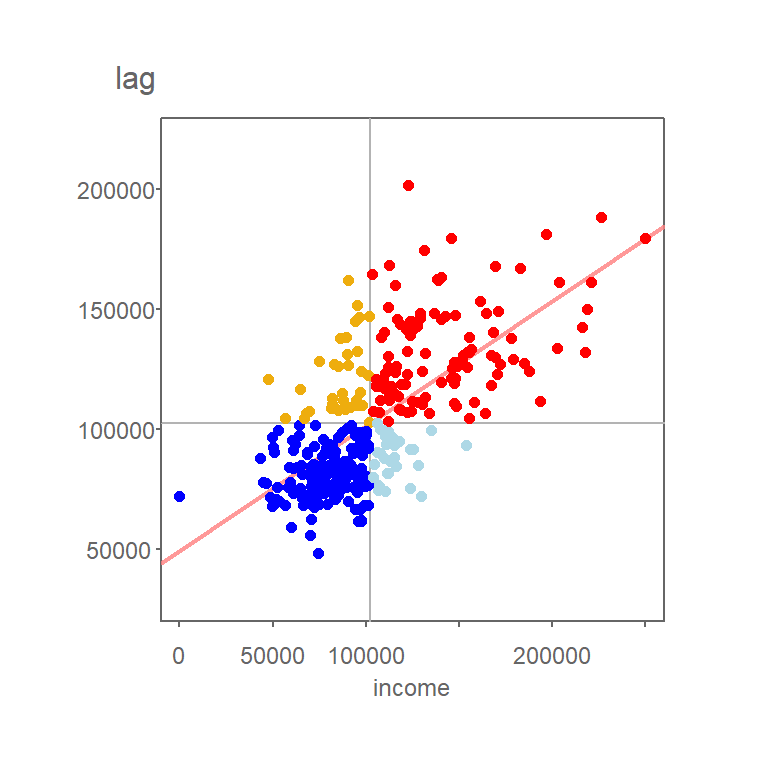
Figure 13.8: Grey vertical and horizontal lines define the mean values for both axes values. Red points highlight counties with relatively high income values (i.e. greater than the mean) surrounded by counties whose average income value is relatively high. Likewise, dark blue points highlight counties with relatively low income values surrounded by counties whose average income value is relatively low.

Note that the mean value for Income, highlighted as light grey vertical and horizontal lines in the above plot, carve up the four quadrant defining the low-low, high-low, high-high and low-high quadrants when starting from the bottom-left quadrant and working counterclockwise. Note that other measures of centrality, such as the median, could be used to delineate these quadrants.

The values in the above scatter plot can be mapped to each polygon in the dataset as shown in the following figure.

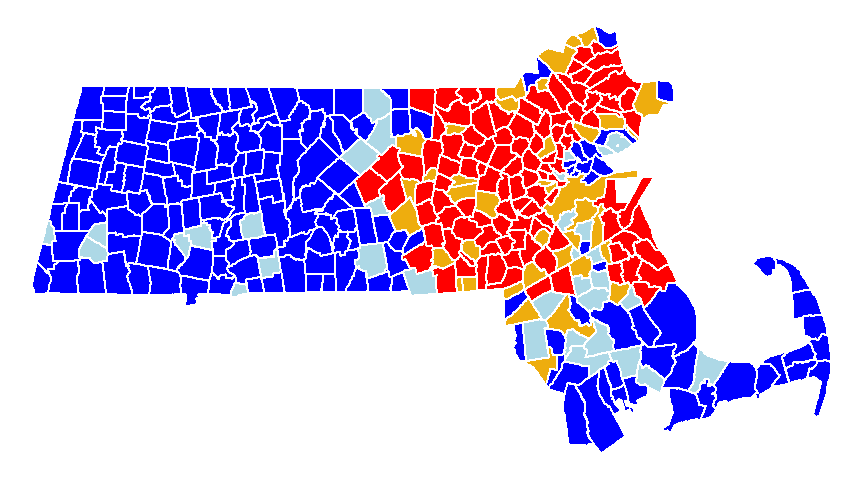
Figure 13.9: A map view of the low-low (blue), high-low (light-blue), high-high (red) and low-high (orange) counties.

Each spatial unit (e.g., polygon) has its own Local Moran’s I statistic, denoted \(I_i\), which quantifies the degree of spatial autocorrelation around that unit. The calculation of \(I_i\) is shown later in the chapter.

While the scatterplot helps visually identify potential clusters, statistical significance must be assessed to determine whether these patterns are likely to have occurred by chance.

As with the global Moran’s I, there is both an analytical and Monte Carlo approach to computing significance of \(I_i\). In the case of a Monte Carlo approach, the values of all other units are shuffled while keeping the value of unit \(i\) fixed. For each permutation, a new \(I_i\) is computed based on the randomized neighborhood values. For each permutation, we compare the value at \(y_i\) to the average value of its neighboring values. From the permutations, we generate a distribution of \(I_i\) values (for each \(y_i\) feature) we would expect to get if the values were randomly distributed across all features.

To illustrate, consider a polygon in eastern Massachusetts with a high observed \(I_i\) value. We assess its significance by comparing it to a distribution of \(I_i\) values generated through permutation.

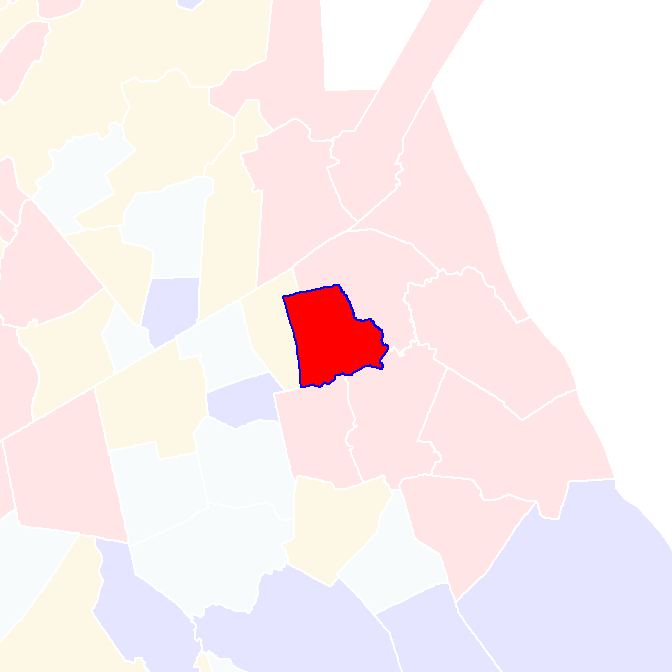
Figure 13.10: Polygon whose significance value we are asessing in this example.

Its local Moran’s I statistic is 0.85. A permutation test shuffles the income values around it, all the while keeping its value constant. An example of an outcome of a few permutations follows:

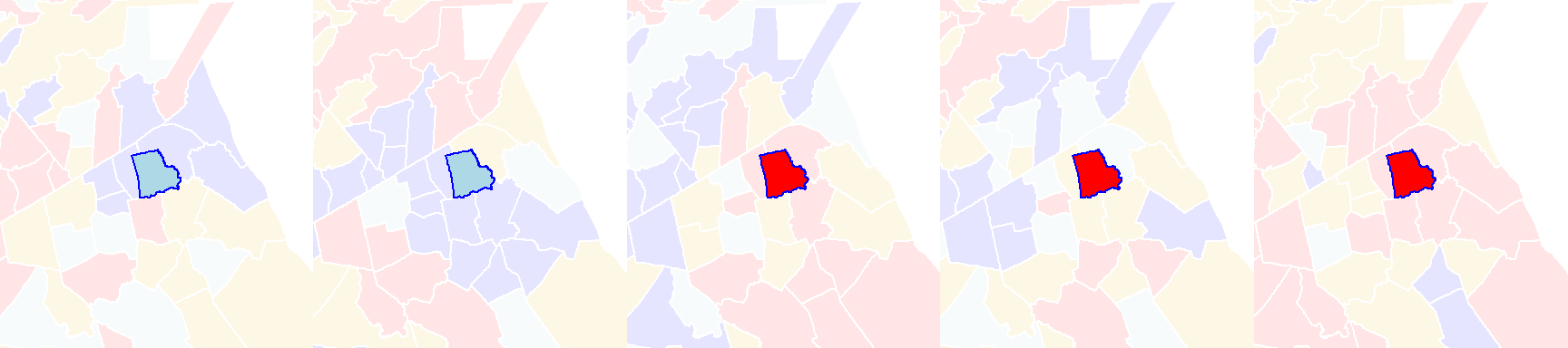
Figure 13.11: Local Moran’s I outcomes of a few permutations of income values.

You’ll note that even though the income value remains the same in the polygon of interest, its local Moran’s I statistic will change because of the changing income values in its surrounding polygons.

If we perform many more permutations, we come up with a distribution of \(I_i\) values under the null that the income values are randomly distributed across the state of Massachusetts. The distribution of \(I_i\) for the above example is plotted using a histogram.

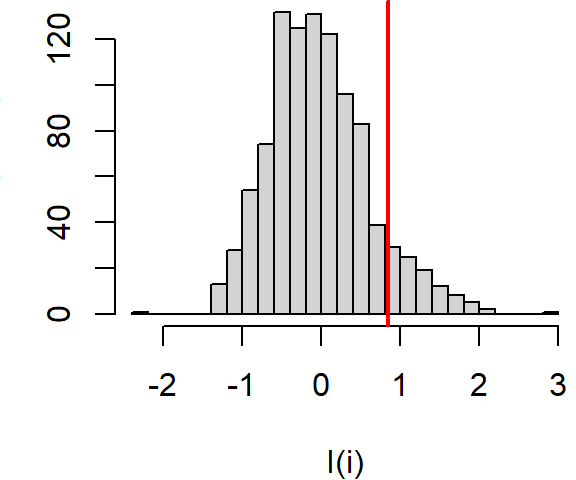
Figure 13.12: Distribution of \(I_i\) values under the null hypothesis that income values are randomly distributed across the study extent. The red vertical line shows the observed \(I_i\) for comparison.

About 9.3% of the simulated values are more extreme than our observed \(I_i\) giving us a permutation-based p-value of 0.09.

If we perform this permutation for all polygons in our dataset, we can map the permutation-based p-values for each polygon. Note that here, we are mapping the probability that the observed \(I_i\) value is more extreme than expected (equivalent to a one-tail test).

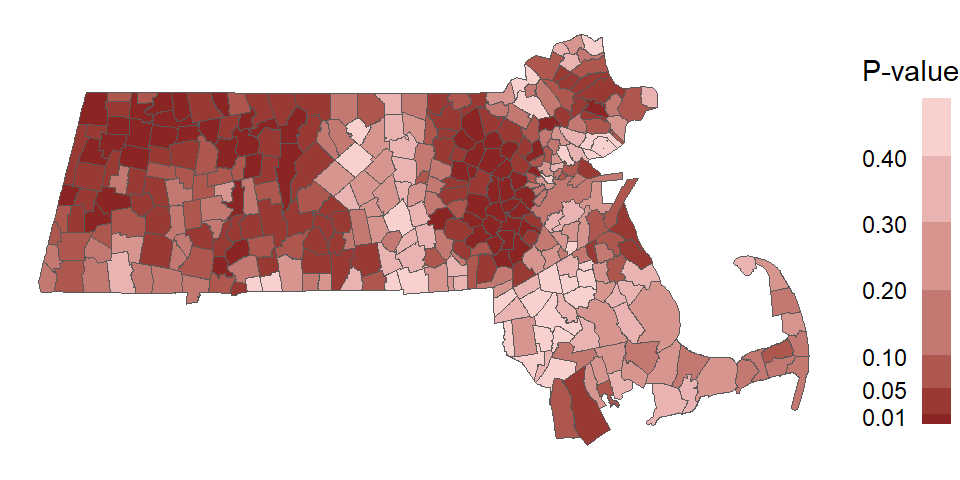
Figure 13.13: Map of the permutation-based p-values for each polygons’ \(I_i\) statistic.

One can use the computed permutation-based p-values to filter the \(I_i\) values based on a desired level of significance. For example, the following scatter plot and map shows the high/low “hotspots” for which a permutation-based p-value of 0.05 or less was computed from the above simulation.

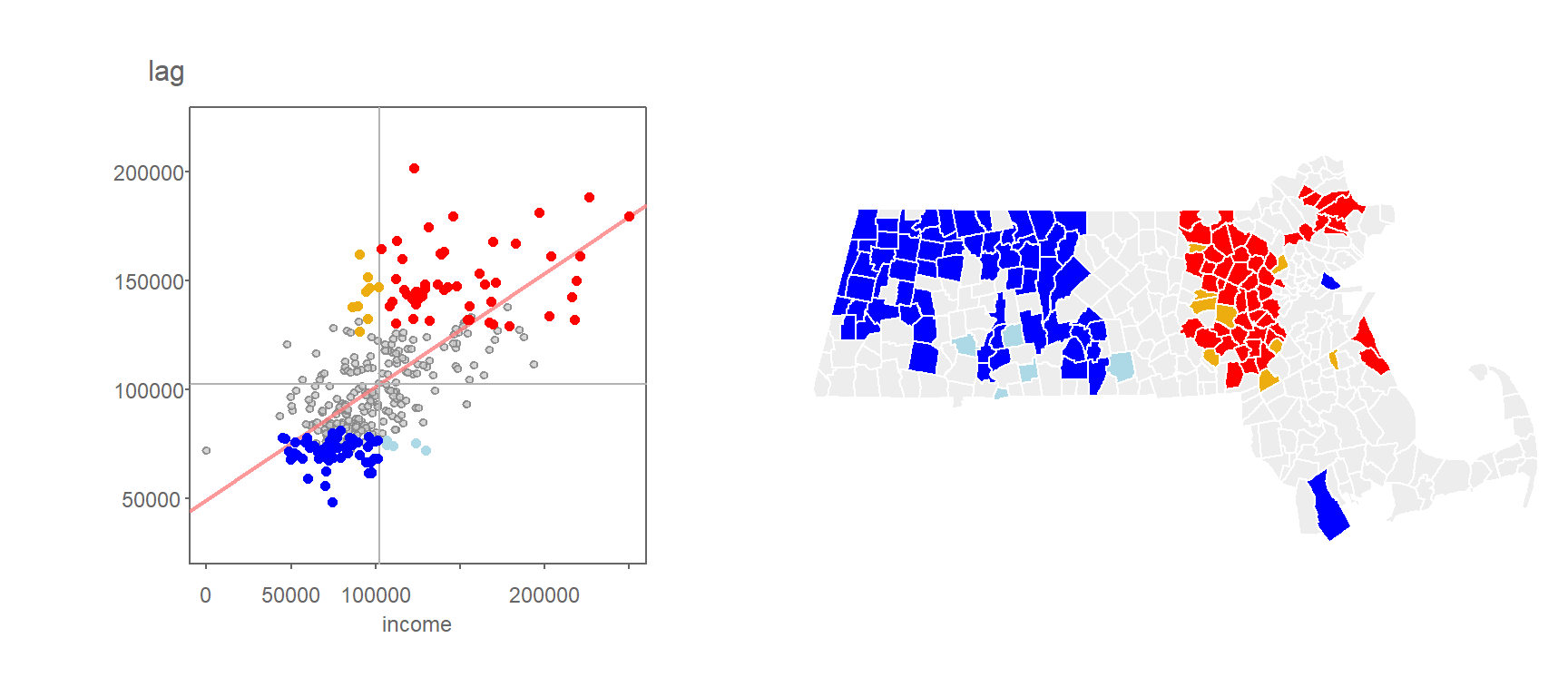
Figure 13.14: Local Moran’s I values having a signifcance level of 0.05 or less.

You’ll note that the levels of significance do not apply to just the high-high and low-low regions, they can apply to all combinations of highs and lows.

Another example, where the \(I_i\) values are filtered based on a more stringent significance level of 0.01, is shown in the following figure.

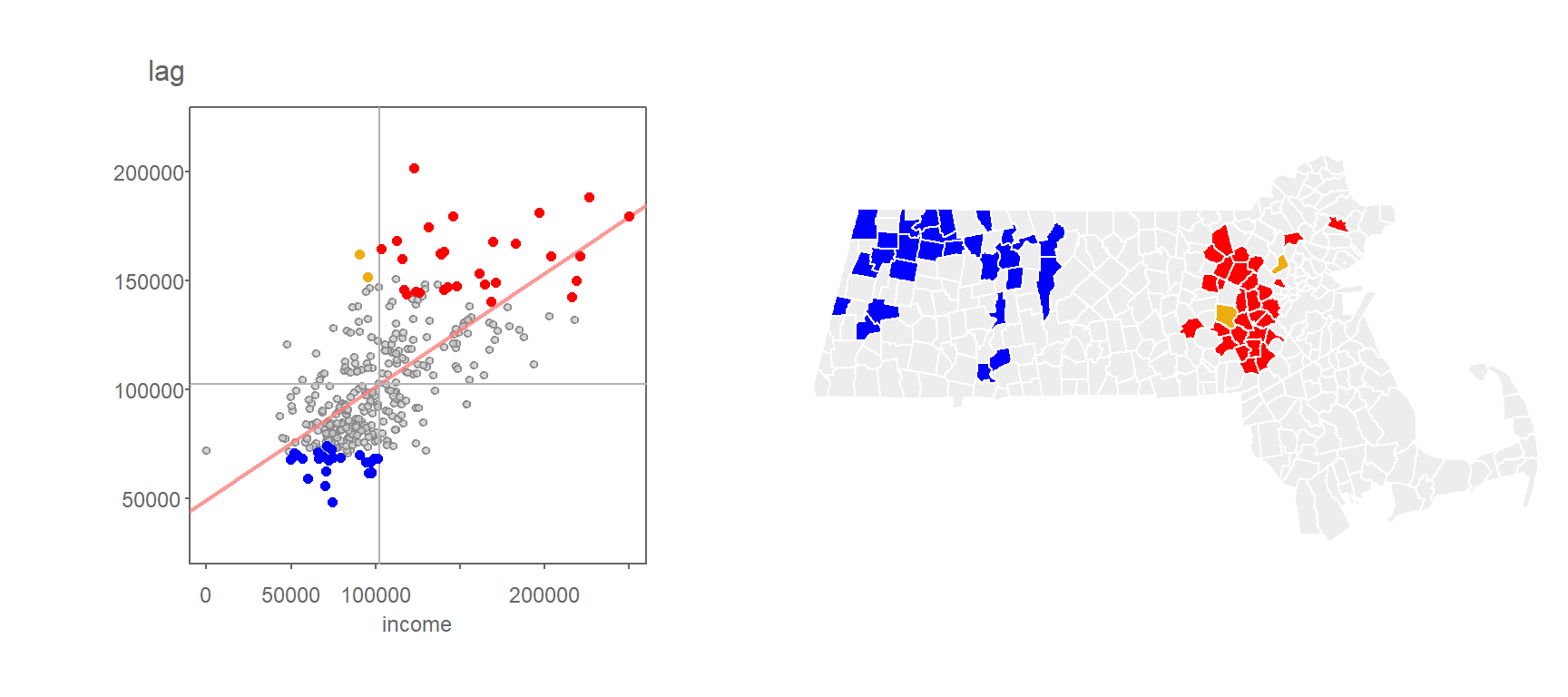
Figure 13.15: Local Moran’s I values having a signifcance level of 0.01 or less.

13.4.1 A note about interpreting the permutation-based p-value

While the permutation technique highlighted in the previous section used in assessing the significance of localized spatial autocorrelation does a good job in circumventing limitations found in a parametric approach to inference (e.g. skewness in the data, irregular grids, etc…), it still has some limitations when one interprets this level of significance across all features. For example, if the underlying process that generated the distribution of income values was truly random, the outcome of such a realization could look like this:

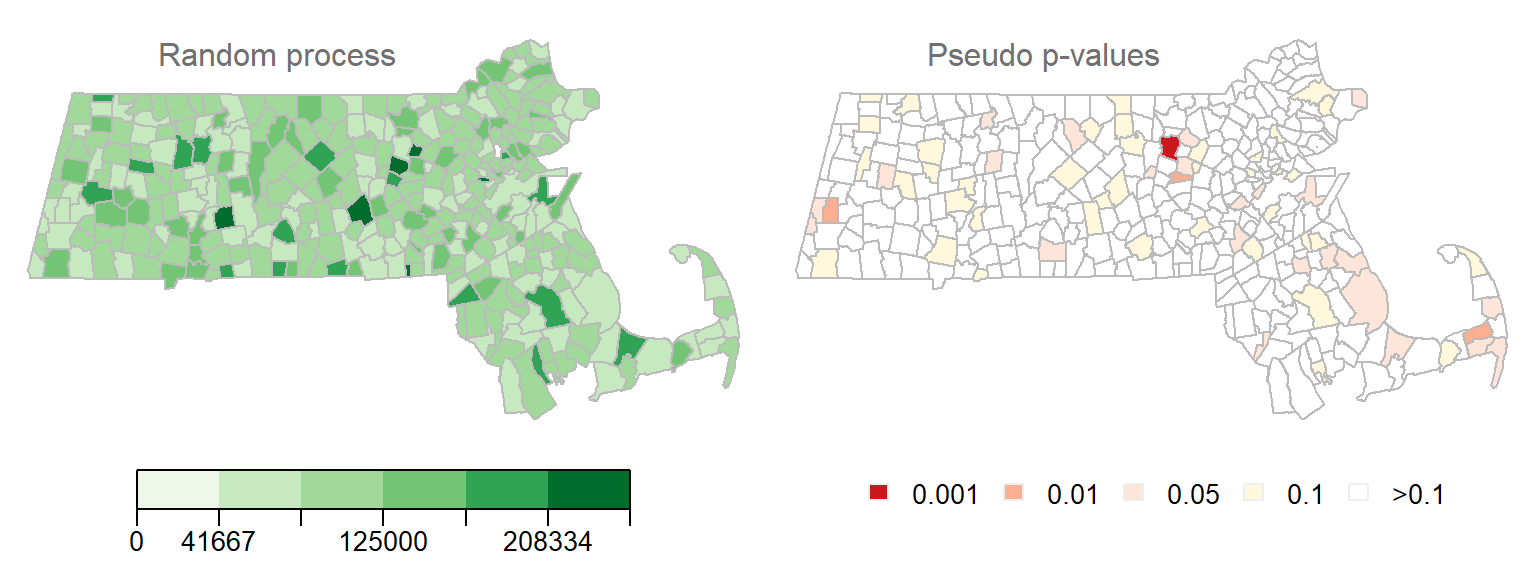
Figure 13.16: Realization of a random process. Left map is the distribution of income values under a random process. Right map is the outcome of a permutation test showing the computed permutation-based p-values. Each permutation test runs 9999 permutations.

Note how some \(I_i\) values are associated with low permutation-based p-value. In fact, one polygon’s \(I_i\) value is associated with permutation-based p-value of 0.001 or less! This is to be expected since the likelihood of finding a significant \(I_i\) increases the more permutation tests are performed. Here we have 343 polygons, thus we ran 343 tests. This is analogous to having multiple opportunities to pick an ace of spades from a deck of cards–the more opportunities you have, the greater the chance of grabbing an ace of spades.

Another example of a local Moran’s I test on a realization of a randomly reshuffled set of income values is shown next:

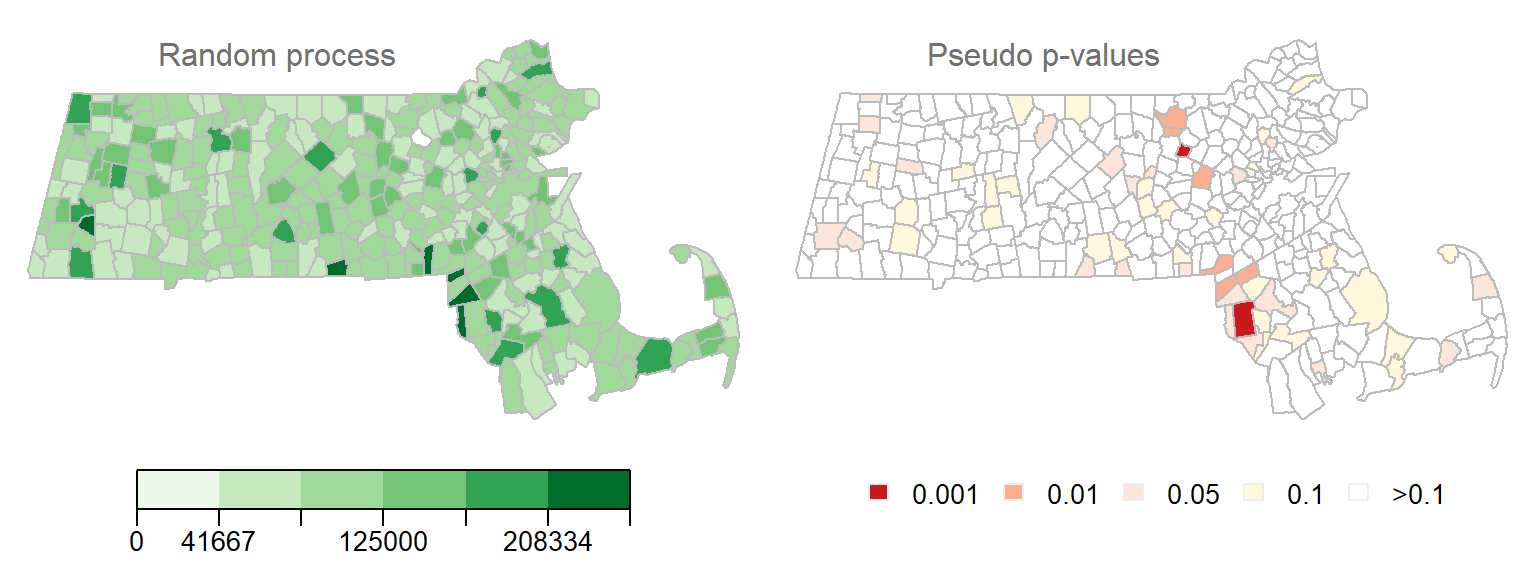
Figure 13.17: Another realization of a random process. Left map is the distribution of income values under a random process. Right map is the outcome of a permutation test showing computed permutation-based p-values.

We have quite a few \(I_i\) values associated with a very low permutation-based p-value (The smallest p-value in this example is 0.0006). This would lead one to assume that several polygons exhibit significant levels of spatial autocorrelation with their neighbors when in fact this is due to chance–a classic example of a Type I error resulting from multiple comparisons.

To further illustrate the issue, consider generating 200 independent realizations of a random spatial process. Each realization involves computing permutation-based p-values for all polygons, resulting in a large number of tests and an increased likelihood of false positives. This generates 200 x 323 permutation-based p-values. With this working example, about 10% of the outcomes result in a permutation-based p-value of 0.05 or less.

Figure 13.18: Distribution of permutation-based p-values following 200 realizations of a random process. Blue numbers are the p-value bins, red numbers under each bins are calculated percentages.

This problem is known in the field of statistics as the multiple comparison problem. Several solutions have been offered, each with their pros and cons. One solution that seems to have gained traction as of late is the False Discoverer Rate correction (FDR). The FDR correction aims to control the expected proportion of false positives among the set of features deemed significant.

There are at least a couple of different implementation of FDR. One implementation starts by ranking the permutation-based p-values, \(p\), from smallest to largest and assigning a rank, \(i\), to each value. Next, a reference value is computed for each rank as \(i(\alpha/n)\) where \(\alpha\) is the desired significance cutoff value (0.05, for example) and \(n\) is the total number of observations (e.g. polygons) for which a permutation-based p-value has been computed (343 in our working example). All computed \(p_i\) values that are less than \(i(\alpha/n)\) are deemed significant at the desired \(\alpha\) value.

Applying the FDR correction to the permutation-based p-value cutoff of 0.05 in the household income data gives us the following cluster map.

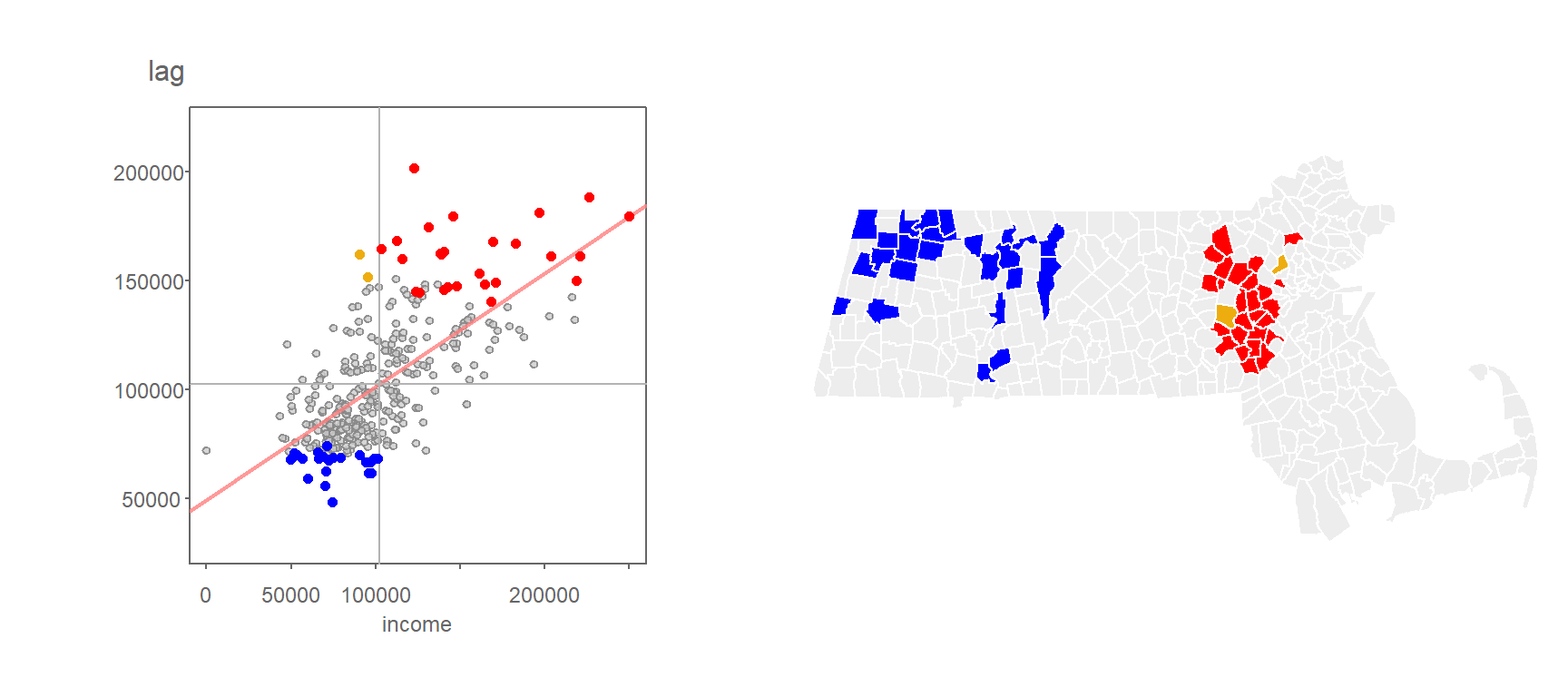
Figure 13.19: Clusters deemed significant at the p=0.05 level when applying the FDR correction.

Applying the FDR correction to the permutation-based p-value cutoff of 0.01 generates even fewer clusters:

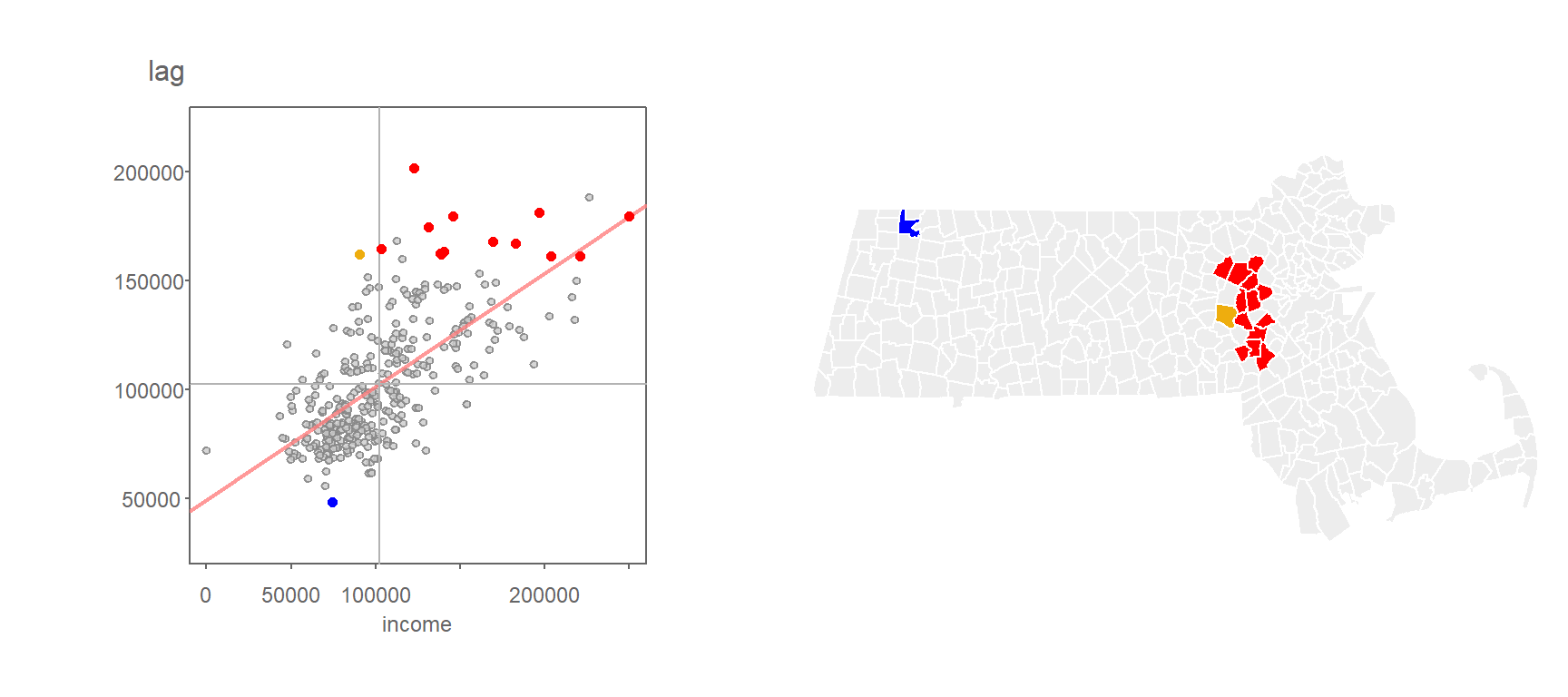
Figure 13.20: Clusters deemed significant at the p=0.01 level when applying the FDR correction.

It’s important to note that there is no one perfect solution to the multiple comparison problem. This, and other challenges facing inferential interpretation in a spatial framework such as the potential for overlapping neighbors (i.e. same polygons used in separate permutation tests) make traditional approaches to interpreting significance challenging. It is thus recommended to interpret these tests with caution.

13.5 Moran’s I equation explained

The Moran’s I statistic can be expressed in several mathematically equivalent forms, each offering different insights into its structure and interpretation. One commonly used formulation is:

\[ I = \frac{N}{\sum\limits_i (X_i-\bar X)^2} \frac{\sum\limits_i \sum\limits_j w_{ij}(X_i-\bar X)(X_j-\bar X)}{\sum\limits_i \sum\limits_j w_{ij}} \tag{1} \]

Here, \(N\) is the total number of spatial units, \(X_i\) and \(X_j\) are the attribute values at locations \(i\) and \(j\), \(\bar{X}\) is the mean of \(X\), and \(w_{ij}\) is the spatial weight between locations \(i\) and \(j\)–typically defined by contiguity, distance, or other spatial relationships.

There are a few key components of Equation (1) worth highlighting. First, you’ll note the standardization of both sets of values by the subtraction of each value in \(X_i\) or \(X_j\) by the mean of \(X\). This highlights the fact that we are seeking to compare the deviation of each value from an overall mean and not the deviation of their absolute values.

Second, you’ll note an inverted variance term on the left-hand side of equation (1): this is a measure of spread. You might recall from an introductory statistics course that the variance can be computed as:

\[ s^2 = \frac{\sum\limits_i (X_i-\bar X)^2}{N}\tag{2} \] Note that a more common measure of variance, the sample variance, where one divides the above numerator by \((n-1)\) can also be adopted in the Moran’s I calculation.

Equation (1) is thus dividing the large fraction on the right-hand side by the variance. This has for effect of limiting the range of possible Moran’s I values between -1 and 1 (note that in some extreme cases, \(I\) can take on a value more extreme than [-1; 1]). We can re-write the Moran’s I equation by plugging in \(s^2\) as follows:

\[ I = \frac{\sum\limits_i \sum\limits_j w_{ij}\frac{(X_i-\bar X)}{s}\frac{(X_j-\bar X)}{s}}{\sum\limits_i \sum\limits_j w_{ij}} \tag{3} \] Note that here \(s\times s = s^2\). You might recognize the numerator as a sum of the product of standardized z-values between neighboring features. If we let \(z_i = \frac{(X_i-\bar X)}{s}\) and \(z_j = \frac{(X_j-\bar X)}{s}\), The Moran’s I equation can be reduced to:

\[ I = \frac{\sum\limits_i \sum\limits_j w_{ij}(z_i\ z_j)}{\sum\limits_i \sum\limits_j w_{ij}} \tag{4} \]

Recall that we are comparing a variable \(X\) at \(i\) to all of its neighboring values at \(j\). More specifically, we are computing a summary value (such as the mean) of the neighboring values at \(j\) and multiplying that by \(X_i\). So, if we let \(y_i = \sum\limits_j w_{ij} z_j\), the Moran’s I coefficient can be rewritten as:

\[ I = \frac{\sum\limits_i z_i y_i}{\sum\limits_i \sum\limits_j w_{ij}} \tag{5} \]

So, \(y_i\) is the average z-value for the neighboring features thus making the product \(z_i y_i\) nothing more than a correlation coefficient.

The product \(z_iy_i\) is a local measure of spatial autocorrelation, \(I_i\). If we don’t summarize across all locations \(i\), we get our local I statistic, \(I_i\):

\[ I_i = z_iy_i \tag{6} \] The global Moran’s I statistic, \(I\), is thus the average of all \(I_i\) values.

\[ I = \frac{\sum\limits_i I_i}{\sum\limits_i \sum\limits_j w_{ij}} \tag{5} \]

Let’s explore elements of the Moran’s I equation using the following sample dataset.

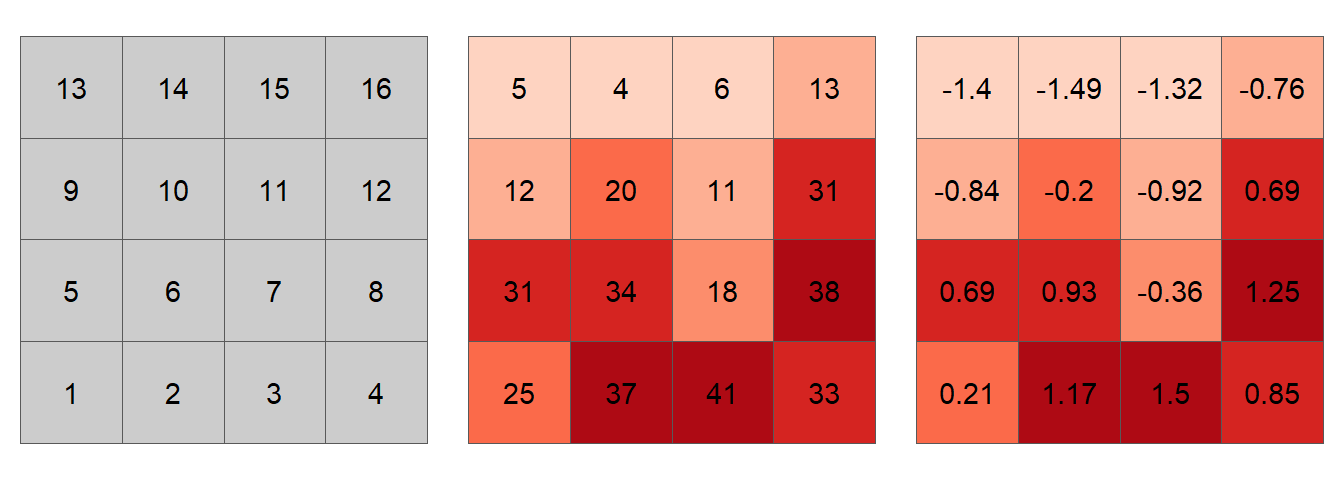
Figure 13.21: Simulated spatial layer. The figure on the left shows each cell’s ID value. The figure in the middle shows the values for each cell. The figure on the right shows the standardized values using equation (2).

The first step in the computation of a Moran’s I index is the generation of a spatial weights matrix. The weights can take on many different values. For example, one could assign a value of 1 to a neighboring cell as shown in the following matrix.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	0	1	0	0	1	1	0	0	0	0	0	0	0	0	0	0
2	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0	0
3	0	1	0	1	0	1	1	1	0	0	0	0	0	0	0	0
4	0	0	1	0	0	0	1	1	0	0	0	0	0	0	0	0
5	1	1	0	0	0	1	0	0	1	1	0	0	0	0	0	0
6	1	1	1	0	1	0	1	0	1	1	1	0	0	0	0	0
7	0	1	1	1	0	1	0	1	0	1	1	1	0	0	0	0
8	0	0	1	1	0	0	1	0	0	0	1	1	0	0	0	0
9	0	0	0	0	1	1	0	0	0	1	0	0	1	1	0	0
10	0	0	0	0	1	1	1	0	1	0	1	0	1	1	1	0
11	0	0	0	0	0	1	1	1	0	1	0	1	0	1	1	1
12	0	0	0	0	0	0	1	1	0	0	1	0	0	0	1	1
13	0	0	0	0	0	0	0	0	1	1	0	0	0	1	0	0
14	0	0	0	0	0	0	0	0	1	1	1	0	1	0	1	0
15	0	0	0	0	0	0	0	0	0	1	1	1	0	1	0	1
16	0	0	0	0	0	0	0	0	0	0	1	1	0	0	1	0

For example, cell ID 1 (whose value is 25 and whose standardized value, \(z_1\), is 0.21) has for neighbors cells 2, 5 and 6. Computationally (working with the standardized values), this gives us a summarized neighboring value (aka lagged value), \(y_1(lag)\) of:

\[ \begin{align*} y_1 = \sum\limits_j w_{1j} z_j {}={} & (0)(0.21)+(1)(1.17)+(0)(1.5)+ ... + \\ & (1)(0.69)+(1)(0.93)+(0)(-0.36)+...+ \\ & (0)(-0.76) = 2.79 \end{align*} \]

Computing the spatially lagged values for the other 15 cells generates the following scatterplot:

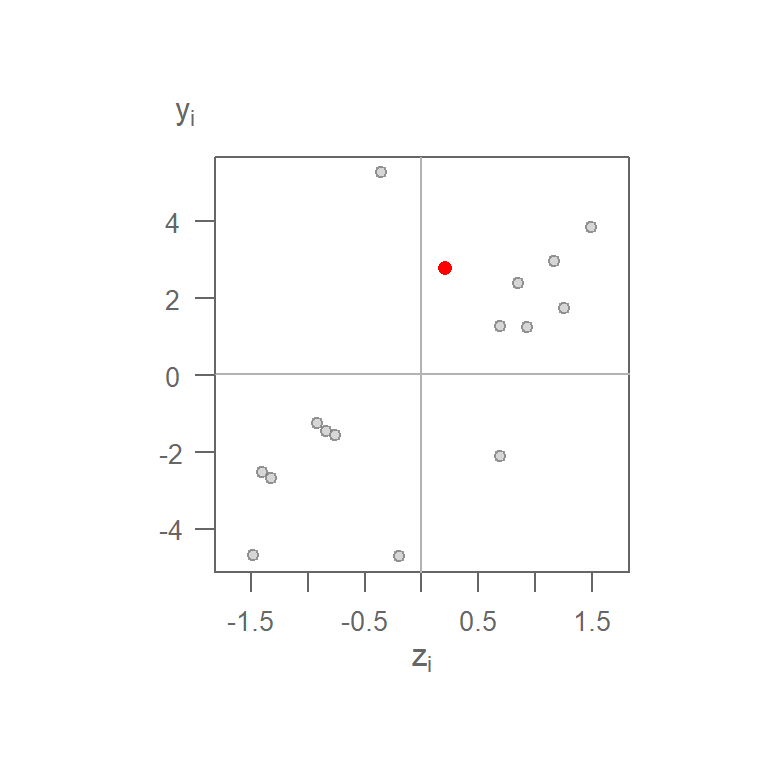
Figure 13.22: Moran’s I scatterplot using a binary weight. The red point is the (\(z_1\), \(y_1\)) pair computed for cell 1.

You’ll note that the range of neighboring values along the \(y\)-axis is much greater than that of the original values on the \(x\)-axis. This is not necessarily an issue given that the Moran’s \(I\) correlation coefficient standardizes the values by recentering them on the overall mean \((X - \bar{X})/s\). This is simply to re-emphasize that we are interested in how a neighboring value varies relative to a feature’s value, regardless of the scale of values in either batches.

If there is a downside to adopting a binary weight, it’s the bias that the different number of neighbors can introduce in the calculation of the spatially lagged values. In other words, a feature with 5 polygons (such as feature ID 12) will have a larger neighboring value than a feature with 3 neighbors (such as feature ID 1) whose neighboring value will be less if there was no spatial autocorrelation in the dataset.

A more natural weight is one where the values are standardized across each row of the weights matrix such that the weights across each row sum to one. For example:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	0	0.333	0	0	0.333	0.333	0	0	0	0	0	0	0	0	0	0
2	0.2	0	0.2	0	0.2	0.2	0.2	0	0	0	0	0	0	0	0	0
3	0	0.2	0	0.2	0	0.2	0.2	0.2	0	0	0	0	0	0	0	0
4	0	0	0.333	0	0	0	0.333	0.333	0	0	0	0	0	0	0	0
5	0.2	0.2	0	0	0	0.2	0	0	0.2	0.2	0	0	0	0	0	0
6	0.125	0.125	0.125	0	0.125	0	0.125	0	0.125	0.125	0.125	0	0	0	0	0
7	0	0.125	0.125	0.125	0	0.125	0	0.125	0	0.125	0.125	0.125	0	0	0	0
8	0	0	0.2	0.2	0	0	0.2	0	0	0	0.2	0.2	0	0	0	0
9	0	0	0	0	0.2	0.2	0	0	0	0.2	0	0	0.2	0.2	0	0
10	0	0	0	0	0.125	0.125	0.125	0	0.125	0	0.125	0	0.125	0.125	0.125	0
11	0	0	0	0	0	0.125	0.125	0.125	0	0.125	0	0.125	0	0.125	0.125	0.125
12	0	0	0	0	0	0	0.2	0.2	0	0	0.2	0	0	0	0.2	0.2
13	0	0	0	0	0	0	0	0	0.333	0.333	0	0	0	0.333	0	0
14	0	0	0	0	0	0	0	0	0.2	0.2	0.2	0	0.2	0	0.2	0
15	0	0	0	0	0	0	0	0	0	0.2	0.2	0.2	0	0.2	0	0.2
16	0	0	0	0	0	0	0	0	0	0	0.333	0.333	0	0	0.333	0

The spatially lagged value for cell ID 1 is thus computed as:

\[ \begin{align*} y_1 = \sum\limits_j w_{1j} z_j {}={} & (0)(0.21)+(0.333)(1.17)+(0)(1.5)+...+ \\ & (0.333)(0.69)+(0.333)(0.93)+(0)(-0.36)+...+ \\ & (0)(-0.76) = 0.93 \end{align*} \]

Multiplying each neighbor by the standardized weight, then summing these values, is simply computing the neighbor’s mean value.

Using the standardized weights generates the following scatter plot. Plot on the left shows the raw values on the x and y axes; plot on the right shows the standardized values \(z_i\) and \(y_i = \sum\limits_j w_{ij} z_j\). You’ll note that the shape of the point cloud is the same in both plots given that the axes on the left plot are scaled such as to match the standardized scales in both axes.

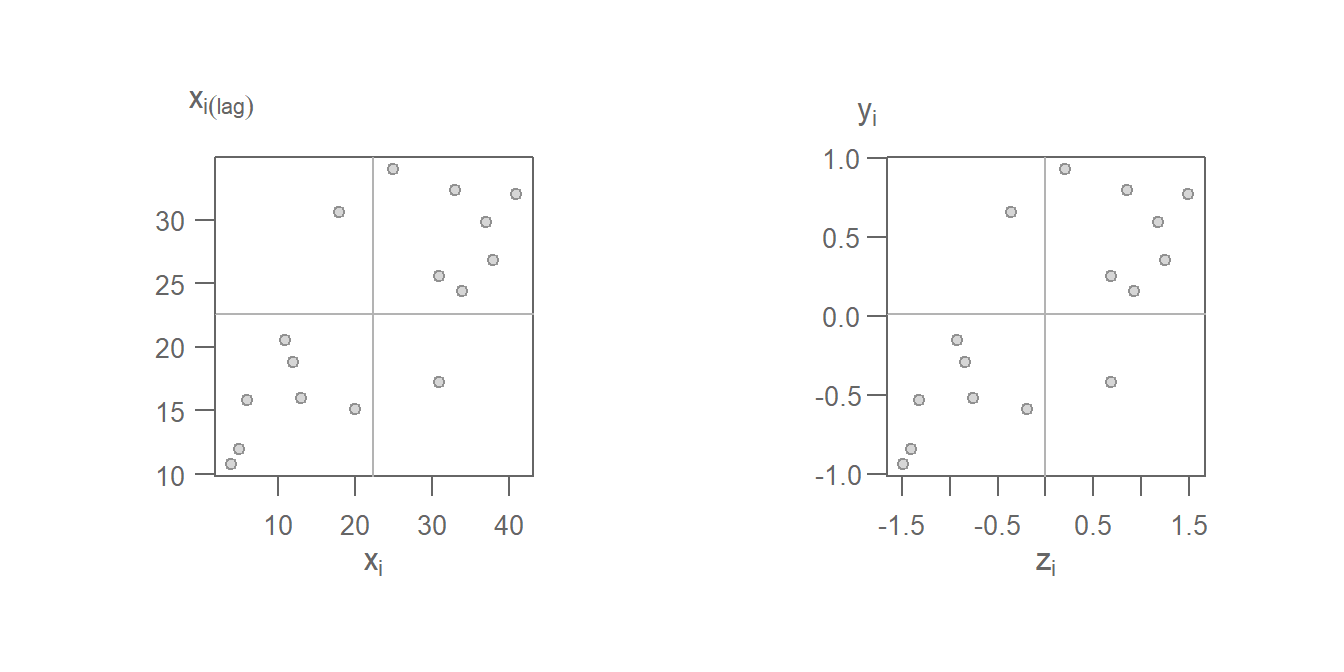
Figure 13.23: Moran’s scatter plot with original values on the left and same Moran’s I scatter plot on the right using the standardized values \(z_i\) and \(y_i\).

Note the difference in the point cloud pattern in the above plot from the one generated using the binary weights. Other weights can be used such as inverse distance and k-nearest neighbors to name just a few. However, must software implementations of the Moran’s I statistic will adopt the row standardized weights.

13.5.1 Local Moran’s I

Once a spatial weight is chosen, and both \(z_i\) and \(y_i\) are computed. We can compute the \(z_iy_i\) product for all locations of \(i\) thus giving us a measure of the local Moran’s I statistic. Taking feature ID of 1 in our example, we compute \(I_1(lag) = 0.21 \times 0.93 = 0.19\). Computing \(I_i\) for all cells gives us the following plot.

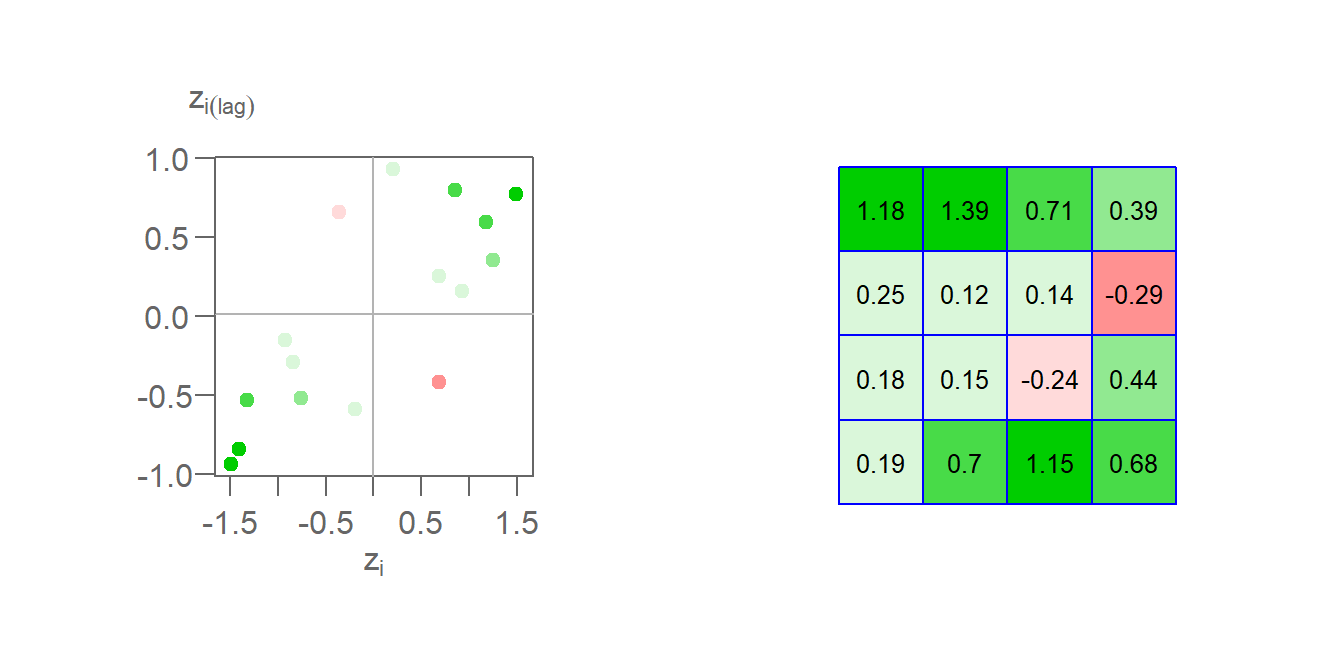
Figure 13.24: The left plot shows the Moran’s I scatter plot with the point colors symbolizing the \(I_i\) values. The figure on the right shows the matching \(I_i\) values mapped to each respective cell.

Here, we are adopting a different color scheme from that used earlier. Green colors highlight features whose values are surrounded by similar values. These can be either positive values surrounded by standardized values that tend to be positive or negative values surrounded by values that tend to be negative. In both cases, the calculated \(I_i\) will be positive. Red colors highlight features whose values are surrounded by dissimilar values. These can be either negative values surrounded by values that tend to be positive or positive values surrounded by values that tend to be negative. In both cases, the calculated \(I_i\) will be negative. In our example, two features have a negative Moran’s I coefficient: cell IDs 7 and 12.

13.5.2 Global Moran’s I

The Global Moran’s I coefficient, \(I\) is nothing more than a summary of the local Moran’s I coefficients. Using a standardized weight, \(I\) is the average of all \(I_i\) values.

\[ \begin{pmatrix} \frac{0.19+0.7+1.15+0.68+0.18+0.15+-0.24+0.44+0.25+0.12+0.14+-0.29+1.18+1.39+0.71+0.39}{\sum\limits_i\sum\limits_j w_{ij}} = 0.446 \end{pmatrix} \] In this example, \(\sum\limits_i \sum\limits_j w_{ij}\) is the sum of all 256 values in Table (2) which, using standardized weights, sums to 16.

\(I\) is thus the slope that best fits the data. This can be plotted using either the standardized values or the raw values.

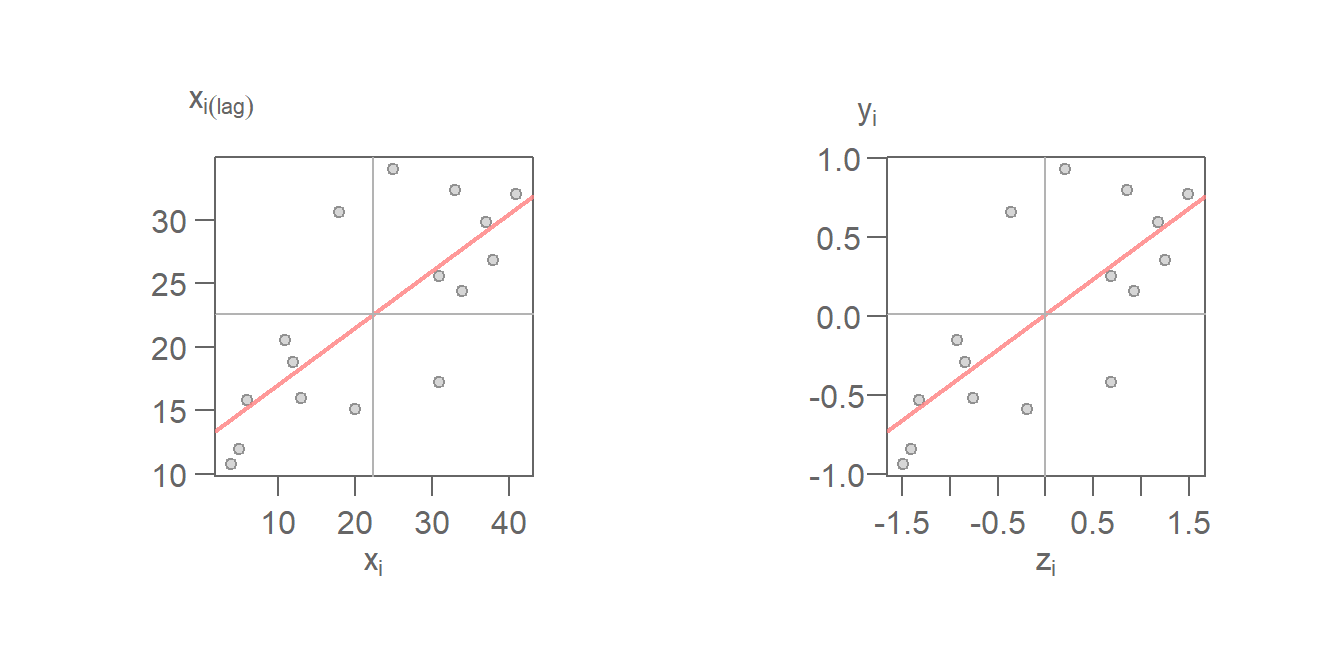
Figure 13.25: Moran’s scatter with fitted Moran’s I slope (red line). The left plot uses the raw values \((X_i,X_i(lag))\) for its axes labels. Right plot uses the standardized values \((z_i,y_i)\) for its axes labels.

13.6 Summary

This chapter introduced spatial autocorrelation as a key concept for understanding second-order spatial structure: how values at one location relate to values at nearby locations. Using Moran’s I as a central tool, we explored both global and local measures of spatial association, emphasizing the importance of spatial weights and neighborhood definitions. Through examples and permutation-based inference, we demonstrated how spatial autocorrelation can be quantified, tested, and interpreted across scales. The chapter concluded with a detailed breakdown of the Moran’s I equation, reinforcing its interpretation as a spatially weighted correlation.

References

Tobler, Waldo R. 1970. “A Computer Movie Simulating Urban Growth in the Detroit Region.” Economic Geography 46 (2): 234–40. http://www.geog.ucsb.edu/~tobler/publications/pdf_docs/A-Computer-Movie.pdf.